1
Tools for Analysis of Dynamic
Systems: Lyapunov’s Methods
Stanisław H. Żak
School of Electrical and
Computer Engineering
ECE 680
Fall 2013

2
A. M. Lyapunov’s (1857--1918) Thesis

3
Lyapunov’s Thesis

4
Lyapunov’s Thesis Translated

5
Some Details About Translation

6
Outline
Notation using simple examples of
dynamical system models
Objective of analysis of a nonlinear
system
Equilibrium points
Lyapunov functions
Stability
Barbalat’s lemma

7
A Spring-Mass Mechanical System
x---displacement of the mass from
the rest position

8
Modeling the Mass-Spring System
Assume a linear mass, where k is the
linear spring constant
Apply Newton’s law to obtain
Define state variables: x
1
=x and x
2
=dx/dt
The model in state-space format:

9
Analysis of the Spring-Mass System
Model
The spring-mass system model is linear
time-invariant (LTI)
Representing the LTI system in standard
state-space format

10
Modeling of the Simple Pendulum
The simple pendulum

11
The Simple Pendulum Model
Apply Newton’s second law
where J is the moment of inertia,
Combining gives
sinmglJ
2
mlJ
sin
l
g

12
State-Space Model of the Simple
Pendulum
Represent the second-order differential
equation as an equivalent system of two
first-order differential equations
First define state variables,
x
1
=θ and x
2
=dθ/dt
Use the above to obtain state–space
model (nonlinear, time invariant)

13
Objectives of Analysis of Nonlinear Systems
Similar to the objectives pursued when
investigating complex linear systems
Not interested in detailed solutions, rather
one seeks to characterize the system
behavior---equilibrium points and their
stability properties
A device needed for nonlinear system
analysis summarizing the system
behavior, suppressing detail

14
Summarizing Function (D.G.
Luenberger, 1979)
A function of the system state
vector
As the system evolves in time,
the summarizing function takes
on various values conveying
some information about the
system

15
Summarizing Function as a First-Order
Differential Equation
The behavior of the summarizing
function describes a first-order
differential equation
Analysis of this first-order
differential equation in some
sense a summary analysis of the
underlying system

16
Dynamical System Models
Linear time-invariant (LTI) system model
Nonlinear system model
Shorthand notation of the above model
nn
A,Axx
n
xxtfx ,,
nn
n
n
n
x,,x,tf
x,,x,tf
x,,x,tf
x
x
x
1
12
11
2
1

17
More Notation
System model
Solution
Example: LTI model,
Solution of the LTI modeling equation
00
xtx,tx,tftx
00
x,t;txtx
0
0 xx,Axx
0
xetx
At

18
Equilibrium Point
A vector is an equilibrium point for a
dynamical system model
if once the state vector equals to it remains
equal to for all future time. The equilibrium
point satisfies
e
x
tx,tftx
e
x
e
x
0, txtf

19
Formal Definition of Equilibrium
A point x
e
is called an equilibrium
point of dx/dt=f(t,x), or simply
an equilibrium, at time t
0
if for
all t ≥ t
0,
f(t, x
e
)=0
Note that if x
e
is an equilibrium
of our system at t
0
, then it is
also an equilibrium for all τ ≥ t
0

20
Equilibrium Points for LTI Systems
For the time invariant system
dx/dt=f(x)
a point is an equilibrium at some
time τ if and only if it is an
equilibrium at all times

21
Equilibrium State for LTI Systems
LTI model
Any equilibrium state must satisfy
If exist, then we have unique equilibrium
state
Axx,tfx
0
e
Ax
e
x
1
A
0
e
x

22
Equilibrium States of Nonlinear
Systems
A nonlinear system may have a
number of equilibrium states
The origin, x=0, may or may not
be an equilibrium state of a
nonlinear system

23
Translating the Equilibrium of
Interest to the Origin
If the origin is not the
equilibrium state, it is always
possible to translate the origin of
the coordinate system to that
state
So, no loss of generality is lost in
assuming that the origin is the
equilibrium state of interest

24
Example of a Nonlinear System with
Multiple Equilibrium Points
Nonlinear system model
Two isolated equilibrium states
2
121
2
2
1
xxx
x
x
x
0
1
0
0
21
ee
xx

25
Isolated Equilibrium
An equilibrium point x
e
in R
n
is
an isolated equilibrium point if
there is an r>0 such that the r-
neighborhood of x
e
contains no
equilibrium points other than x
e

26
Neighborhood of
x
e
The r-neighborhood of x
e
can be
a set of points of the form
where ||.|| can be any p-norm
on R
n

27
Remarks on Stability
Stability properties characterize
the system behavior if its initial
state is close but not at the
equilibrium point of interest
When an initial state is close to
the equilibrium pt., the state
may remain close, or it may
move away from the equilibrium
point

28
An Informal Definition of Stability
An equilibrium state is stable if
whenever the initial state is near
that point, the state remains
near it, perhaps even tending
toward the equilibrium point as
time increases

29
Stability Intuitive Interpretation

30
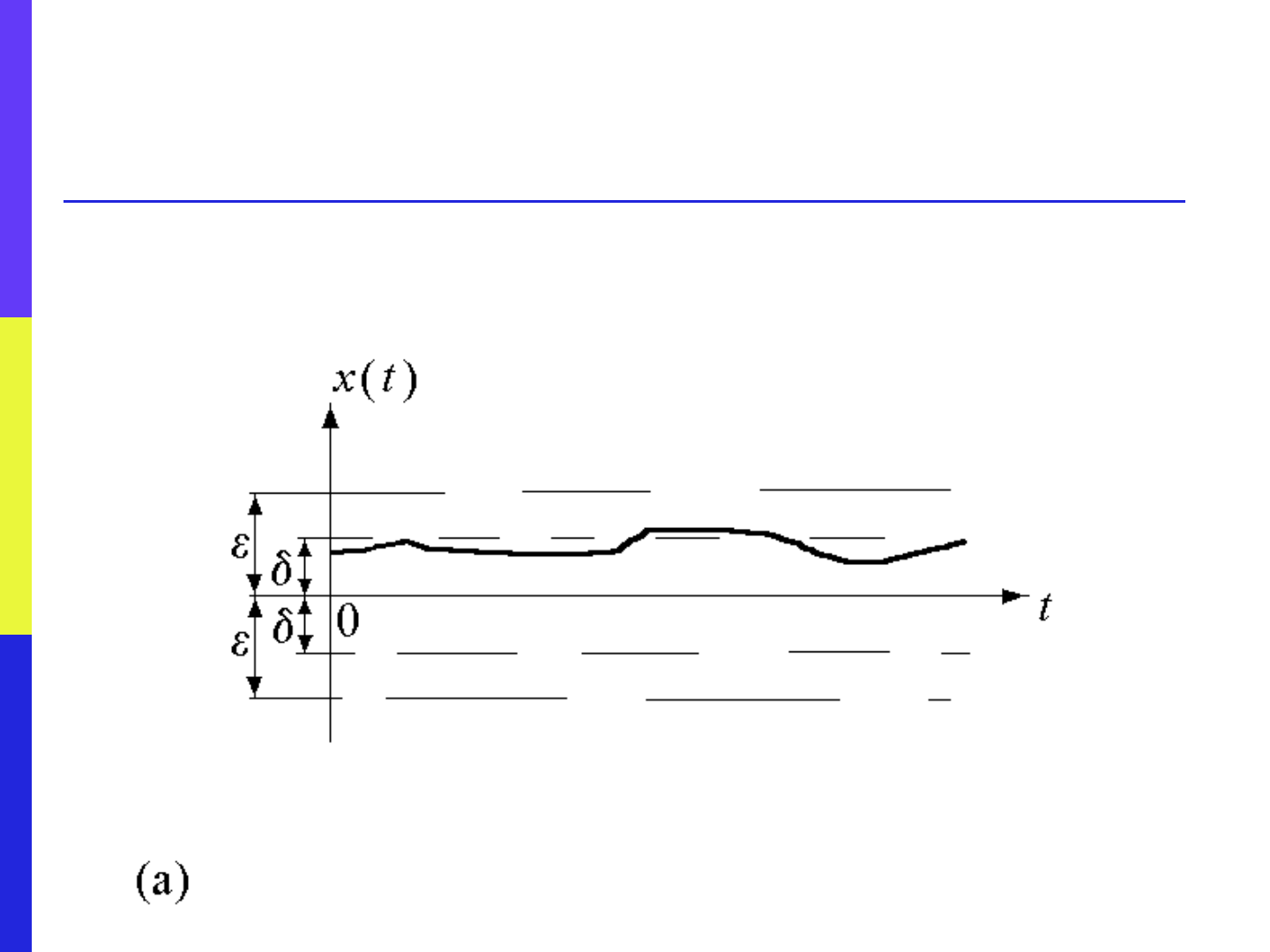
Formal Definition of Stability
An equilibrium state is stable, in the sense
of Lyapunov, if for any given and any positive
scalar there exist a positive scalar
such that if
then
for all
eq
x
0
t
,
0
t
e
xxttx
00
,;
e
xtx
0
0
tt
31
Stability Concept in 1D

32
Stability Concepts in 2D

33
Further Discussion of Lyapunov
Stability
Think of a contest between you,
the control system designer, and
an adversary (nature?)---B.
Friedland (ACSD, p. 43, Prentice-
Hall, 1996)

34
Lyapunov Stability Game
The adversary picks a region in
the state space of radius ε
You are challenged to find a
region of radius δ such that if the
initial state starts out inside your
region, it remains in his region---
if you can do this, your system is
stable, in the sense of Lyapunov

35
Lyapunov Stability---Is It Any
Good?
Lyapunov stability is weak---it
does not even imply that x(t)
converges to x
e
as t approaches
infinity
The states are only required to
hover around the equilibrium
state
The stability condition bounds the
amount of wiggling room for x(t)

36
Asymptotic Stability i.s.L
The property of an equilibrium
state of a differential equation
that satisfies two conditions:
(stability) small perturbations
in the initial condition
produce small perturbations
in the solution;

37
Second Condition for Asymptotic
Stability of an Equilibrium
(attractivity of the equilibrium
point) there is a domain of
attraction such that whenever
the initial condition belongs to
this domain the solution
approaches the equilibrium state
at large times

38
Asymptotic Stability in the sense of
Lyapunov (i.s.L.)
The equilibrium state is
asymptotically stable if
it is stable, and
convergent, that is,
tasxx,t;tx
e00

39
Convergence Alone Does Not
Guarantee Asymptotic Stability
Note: it is not sufficient that just
for asymptotic stability. We need
stability too! Why?
tasxx,t;tx
e00

40
How Long to the Equilibrium?
Asymptotic stability does not
imply anything about how long it
takes to converge to a
prescribed neighborhood of x
e
Exponential stability provides a
way to express the rate of
convergence

41
Asymptotic Stability of Linear
Systems
An LTI system is asymptotically
stable, meaning, the equilibrium
state at the origin is asymptotically
stable, if and only if the eigenvalues
of A have negative real parts
For LTI systems asymptotic stability
is equivalent with convergence
(stability condition automatically
satisfied)

42
Asymptotic Stability of Nonlinear
Systems
For LTI systems asymptotic
stability is equivalent with
convergence (stability condition
automatically satisfied)
For nonlinear systems the state
may initially tend away from the
equilibrium state of interest but
subsequently may return to it

43
Asymptotic Stability in 1D

44
Convergence Does Not Mean
Asymptotic Stability (W. Hahn, 1967)
Hahn’s 1967 Example---A
system whose all solutions are
approaching the equilibrium,
x
e
=0, without this equilibrium
being asymptotically stable
(Antsaklis and Michel, Linear
Systems, 1997, p. 451)

45
Convergence Does Not Mean
Asymptotic Stability (W. Hahn, 1967)
Nonlinear system of Hahn where the origin
is attractive but not a.s.

46
Phase Portrait of Hahn’s 1967 Example

47
Instability in 1D

48
Lyapunov Functions---Basic Idea
Seek an aggregate summarizing
function that continually
decreases toward a minimum
For mechanical systems---
energy of a free mechanical
system with friction always
decreases unless the system is
at rest, equilibrium

49
Lyapunov Function Definition
A function that allows one to
deduce stability is termed a
Lyapunov function

50
Lyapunov Function Properties
for Continuous Time Systems
Continuous-time system
Equilibrium state of interest
txftx
e
x

51
Three Properties of a Lyapunov
Function
We seek an aggregate summarizing
function V
V is continuous
V has a unique minimum with
respect to all other points in some
neighborhood of the equilibrium of
interest
Along any trajectory of the
system, the value of V never
increases

52
Lyapunov Theorem for Continuous
Systems
Continuous-time system
Equilibrium state of interest
txftx
0
e
x

53
Lyapunov Theorem---Negative Rate
of Increase of V
If x(t) is a trajectory, then
V(x(t)) represents the
corresponding values of V along
the trajectory
In order for V(x(t)) not to
increase, we require
0txV

54
The Lyapunov Derivative
Use the chain rule to compute the
derivative of V(x(t))
Use the plant model to obtain
Recall
xxVtxV
T
xfxVtxV
T
T
x
V
x
V
x
V
xV
221

55
Lyapunov Theorem for LTI Systems
The system dx/dt=Ax is
asymptotically stable, that is, the
equilibrium state x
e
=0 is
asymptotically stable (a.s), if
and only if any solution
converges to x
e
=0 as t tends to
infinity for any initial x
0

56
Lyapunov Theorem Interpretation
View the vector x(t) as defining
the coordinates of a point in an
n-dimensional state space
In an a.s. system the point x(t)
converges to x
e
=0

57
Lyapunov Theorem for n=2
If a trajectory is converging to
x
e
=0, it should be possible to
find a nested set of closed curves
V(x
1
,x
2
)=c, c≥0, such that
decreasing values of c yield level
curves shrinking in on the
equilibrium state x
e
=0

58
Lyapunov Theorem and Level
Curves
The limiting level curve
V(x
1
,x
2
)=V(0)=0 is 0 at the
equilibrium state x
e
=0
The trajectory moves through
the level curves by cutting them
in the inward direction ultimately
ending at x
e
=0

59
The trajectory is moving in the
direction of decreasing V
Note that

60
Level Sets
The level curves can be thought
of as contours of a cup-shaped
surface
For an a.s. system, that is, for
an a.s. equilibrium state x
e
=0,
each trajectory falls to the
bottom of the cup

61
Positive Definite Function---General
Definition
The function V is positive definite
in S, with respect to x
e
, if V has
continuous partials, V(x
e
)=0, and
V(x)>0 for all x in S, where x≠x
e

62
Positive Definite Function With
Respect to the Origin
Assume, for simplicity, x
e
=0, then
the function V is positive definite
in S if V has continuous partials,
V(0)=0, and V(x)>0 for all x in S,
where x≠0

63
Example: Positive Definite Function
Positive definite function of two
variables

64
Positive Semi-Definite Function---
General Definition
The function V is positive semi-
definite in S, with respect to x
e
,
if V has continuous partials,
V(x
e
)=0, and V(x)≥0 for all x in
S

65
Positive Semi-Definite Function With
Respect to the Origin
Assume, for simplicity, x
e
=0,
then the function V is positive
semi-definite in S if V has
continuous partials, V(0)=0,
and V(x)≥0 for all x in S

66
Example: Positive Semi-Definite
Function
An example of positive semi-definite
function of two variables
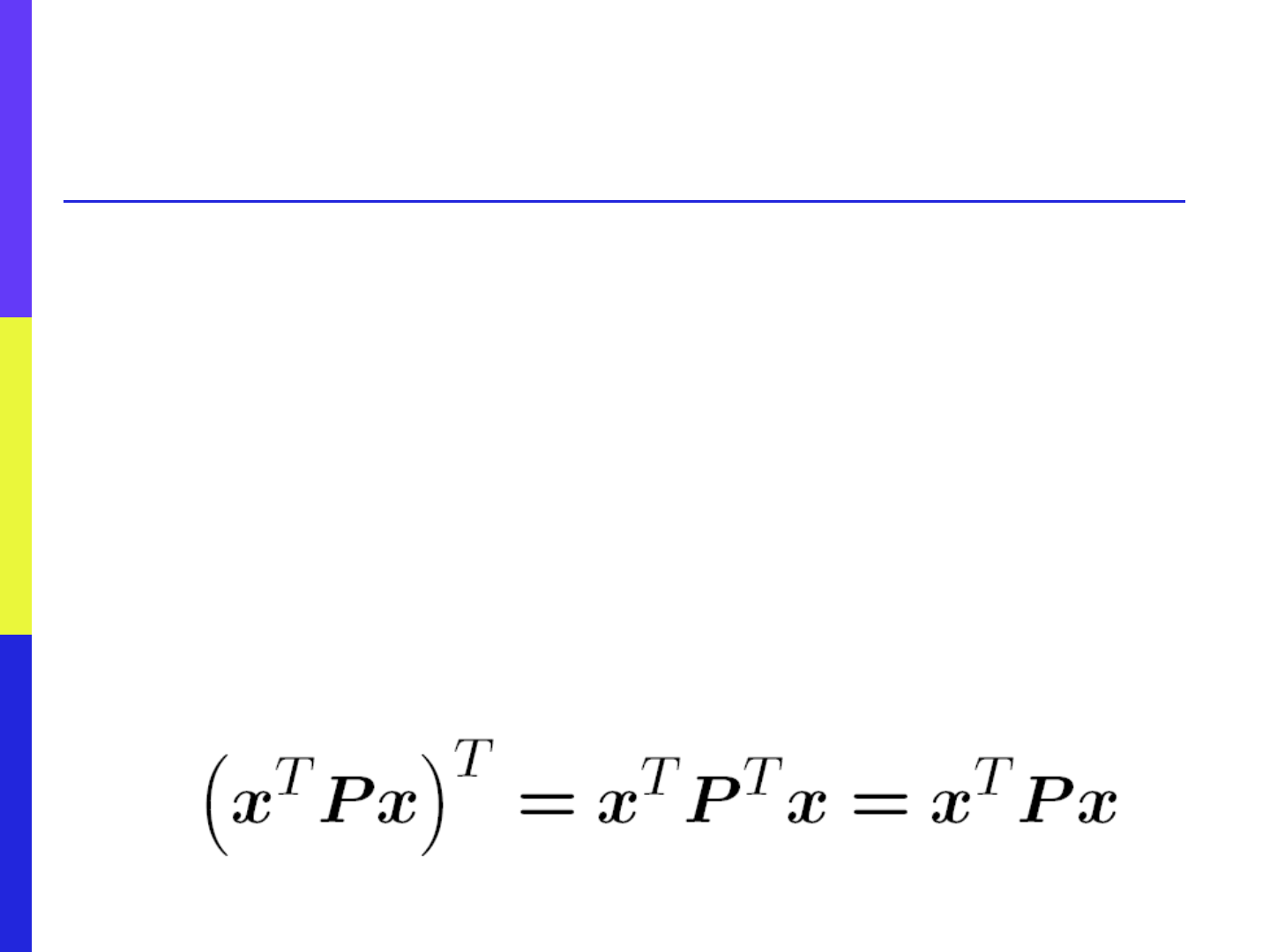
67
Quadratic Forms
V=x
T
Px, where P=P
T
If P not symmetric, need to
symmetrize it
First observe that because the
transposition of a scalar equals
itself, we have

68
Symmetrizing Quadratic Form
Perform manipulations
Note that

69
Tests for Positive and Positive Semi-
Definiteness of Quadratic Form
V=x
T
Px, where P=P
T
, is positive
definite if and only if all
eigenvalues of P are positive
V=x
T
Px, where P=P
T
, is positive
semi-definite if and only if all
eigenvalues of P are non-
negative

70
Comments on the Eigenvalue Tests
These tests are only good for the
case when P=P
T
. You must
symmetrize P before applying
the above tests
Other tests, the Sylvester’s
criteria, involve checking the
signs of principal minors of P

71
Negative Definite Quadratic Form
V=x
T
Px is negative definite if
and only if
-x
T
Px
=
x
T
(-P)x
is positive definite

72
Negative Semi-Definite Quadratic
Form
V=x
T
Px is negative semi-definite
if and only if
-x
T
Px
=
x
T
(-P)x
is positive semi-definite

73
Example: Checking the Sign
Definiteness of a Quadratic Form
Is P, equivalently, is the associated
quadratic form, V=x
T
Px, pd, psd,
nd, nsd, or neither?
The associated quadratic form

74
Example: Symmetrizing the Underlying
Matrix of the Quadratic Form
Applying the eigenvalue test to
the given quadratic form would
seem to indicate that the
quadratic form is pd, which turns
out to be false
Need to symmetrize the
underlying matrix first and then
can apply the eigenvalue test

75
Example: Symetrized Matrix
Symmetrizing manipulations
The eigenvalues of the symmetrized
matrix are: 5 and -1
The quadratic form is indefinite!

76
Example: Further Analysis
Direct check that the quadratic form
is indefinite
Take x=[1 0]
T
. Then
Take x=[1 1]
T
. Then

77
Stability Test for
x
e
=0 of d
x
/dt=
Ax
Let V=x
T
Px where P=P
T
>0
For V to be a Lyapunov function,
that is, for x
e
=0 to be a.s.,
Evaluate the time derivative of V
on the solution of the system
dx/dt=Ax---Lyapunov derivative

78
Lyapunov Derivative for d
x
/dt=
Ax
Note that V(x(t))=x(t)
T
Px(t)
Use the chain rule
We used

79
Lyapunov Matrix Equation
Denote
Then the Lyapunov derivative
can be represented as
where

80
Terms to Our Vocabulary
Theorem---a major result of
independent interest
Lemma---an auxiliary result that is
used as a stepping stone toward a
theorem
Corollary---a direct consequence of a
theorem, or even a lemma

81
Lyapunov Theorem
The real matrix A is a.s., that is,
all eigenvalues of A have
negative real parts if and only if
for any the solution
of the continuous matrix
Lyapunov equation
is (symmetric) positive definite

82
How Do We Use the Lyapunov
Theorem?
Select an arbitrary symmetric
positive definite Q , for example,
an identity matrix, I
n
Solve the Lyapunov equation for
P=P
T
If P is positive definite, the
matrix A is a.s. If P is not p.d.
then A is not a.s.

83
How NOT to Use the Lyapunov
Theorem
It would be no use choosing P to
be positive definite and then
calculating Q
For unless Q turns out to be
positive definite, nothing can be
said about a.s. of A from the
Lyapunov equation
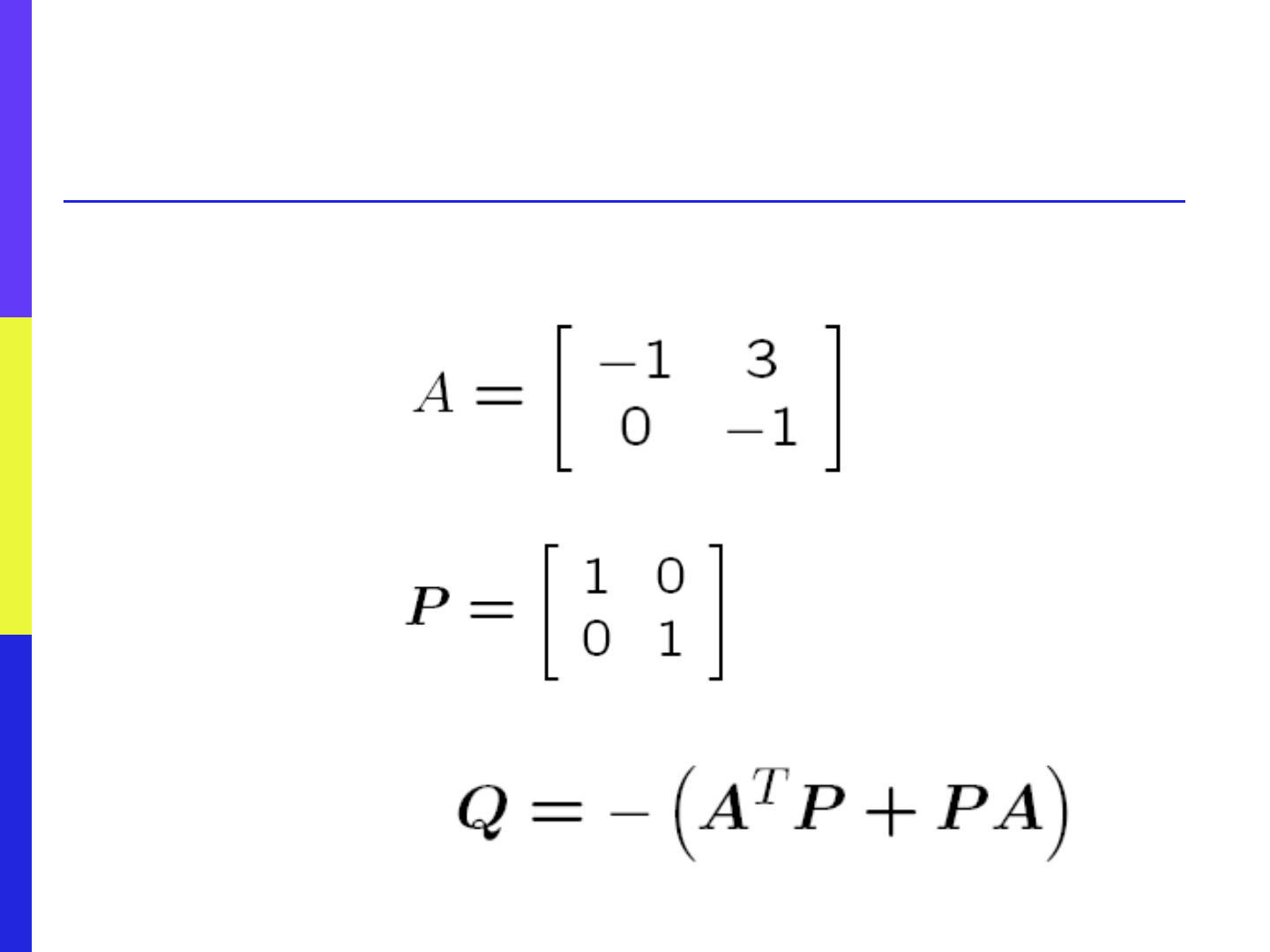
84
Example: How NOT to Use the
Lyapunov Theorem
Consider an a.s. matrix
Try
Compute
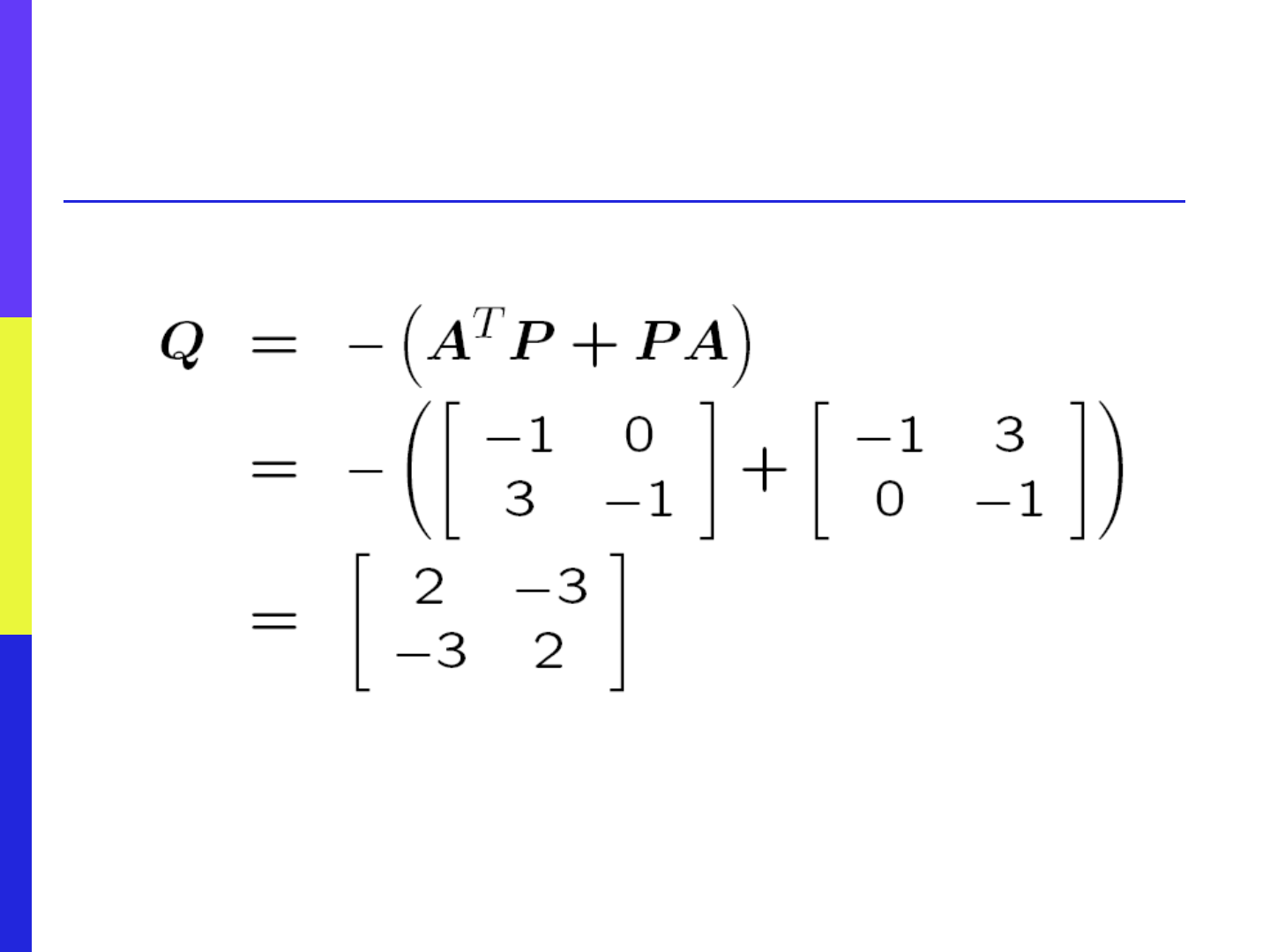
85
Example: Computing
Q
The matrix Q is indefinite!---
recall the previous example

86
Solving the Continuous Matrix
Lyapunov Equation Using MATLAB
Use the MATLAB’s command lyap
Example:
Q=I
2
P=lyap(A,Q)
Eigenvalues of P are positive: 0.2729
and 2.9771; P is positive definite

87
Limitations of the Lyapunov
Method
Usually, it is challenging to analyze
the asymptotic stability of time-
varying systems because it is very
difficult to find Lyapunov functions
with negative definite derivatives
When can one conclude asymptotic
stability when the Lyapunov
derivative is only negative semi-
definite?
88
Some Properties of Time-Varying
Functions
does not imply that f(t)
has a limit as
f(t) has a limit as does not
imply that

89
More Properties of Time-Varying
Functions
If f(t) is lower bounded and
decreasing ( ), then it
converges to a limit. (A well-known
result from calculus.)
But we do not know whether
or not as

90
Preparation for Barbalat’s Lemma
Under what conditions
We already know that the existence
of the limit of f(t) as
is not enough for

91
Continuous Function
A function f(t) is continuous if small
changes in t result in small changes
in f(t)
Intuitively, a continuous function is a
function whose graph can be drawn
without lifting the pencil from the
paper

92
Continuity on an Interval
Continuity is a local property of a
function—that is, a function f is
continuous, or not, at a particular
point
A function being continuous on an
interval means only that it is
continuous at each point of the
interval

93
Uniform Continuity
A function f(t) is uniformly
continuous if it is continuous and, in
addition, the size of the changes in
f(t) depends only on the size of the
changes in t but not on t itself
The slope of an uniformly continuous
function slope is bounded, that is,
is bounded
Uniform continuity is a global
property of a function

94
Properties of Uniformly Continuous
Function
Every uniformly continuous function
is continuous, but the converse is not
true
A function is uniformly continuous, or
not, on an entire interval
A function may be continuous at
each point of an interval without
being uniformly continuous on the
entire interval

95
Examples
Uniformly continuous:
f(t) = sin(t)
Note that the slope of the above
function is bounded
Continuous, but not uniformly
continuous on positive real numbers:
f(t) = 1/t
Note that as t approaches 0, the
changes in f(t) grow beyond any
bound

96
State of an a.s. System With
Bounded Input is Bounded
Example of Slotine and Li, ―Applied
Nonlinear Control,‖ p. 124, Prentice
Hall, 1991
Consider an a.s. stable LTI system
with bounded input
The state x is bounded because u is
bounded and A is a.s.

97
Output of a.s. System With Bounded
Input is Uniformly Continuous
Because x is bounded and u is
bounded, is bounded
Derivative of the output equation is
The time derivative of the output is
bounded
Hence, y is uniformly continuous

98
Barbalat’s Lemma
If f(t) has a finite limit as
and if is uniformly continuous
(or is bounded), then
as

99
Lyapunov-Like Lemma
Given a real-valued function W(t,x)
such that
W(t,x) is bounded below
W(t,x) is negative semi-definite
is uniformly continuous in
t (or bounded) then

100
Lyapunov-Like Lemma---Example;
see p. 211 of the Text
Interested in the stability of the
origin of the system
where u is bounded
Consider the Lyapunov function
candidate

101
Stability Analysis of the System in
the Example
The Lyapunov derivative of V is
The origin is stable; cannot say
anything about asymptotic stability
Stability implies that x
1
and x
2
are
bounded

102
Example: Using the Lyapunov-Like
Lemma
We now show that
Note that V=x
1
2
+x
2
2
is bounded from
below and non-increasing as
Thus V has a limit as
Need to show that is uniformly
continuous

103
Example: Uniform Continuity of
Compute the derivative of and
check if it is bounded
The function is uniformly
continuous because is bounded
Hence
Therefore

104
Benefits of the Lyapunov Theory
Solution to differential equation are
not needed to infer about stability
properties of equilibrium state of
interest
Barbalat’s lemma complements the
Lyapunov Theorem
Lyapunov functions are useful in
designing robust and adaptive
controllers
