
On Linear and Residual Properties
of Graph Products
Tim Hsu & Daniel T. Wise
1. Introduction
Graph groups are groups with presentations where the only relators are commu-
tators of the generators. Graph groups were first investigated by Baudisch [1],
and much subsequent foundational work was done by Droms, B. Servatius, and
H. Servatius [3; 4; 5]. Later, the more general construction of graph products
(Definition 2.1) was introduced and developed by Green [7]. (Graph products are
to free products as graph groups are to free groups.) Graph groups have also been
of recent interest because of their geometric properties (Hermiller and Meier [8]
and VanWyk [13]) and the cohomological properties of their subgroups (Bestvina
and Brady [2]).
In this paper, by embedding graph products in Coxeter groups, we obtain short
proofs of several fundamental properties of graph products. Specifically, after
listing some preliminary definitions and results in Section 2, we show in Sec-
tion 3 that the graph product of subgroups of Coxeter groups is a subgroup of
a Coxeter group (Theorem 3.2). It follows that many classes of graph products
are linear, including graph groups (a result of Humphries [11]) and that the graph
product of residually finite groups is residually finite (a result of Green [7]). In
Section 4, we also include a new and more geometric proof of Green’s normal
form theorem for graph products. Finally, in Section 5, we list some related open
problems.
2. Graph Products
In this section, we review some basic definitions and results on graph products.
For a simplicial graph , we let
0
denote the vertices of , we let
1
denote
the edges of , and we let [v, w] denote the edge between the vertices v and w.
Definition 2.1. Let be a finite simplicial graph, and for each v ∈
0
let G
v
be a group called the vertex group of v. The graph product G
v
is defined to be
the free product of the G
v
, subject to the relations
[g
v
,g
w
] = 1 for all g
v
∈ G
v
,g
w
∈ G
w
such that [v, w]∈
1
. (1)
Received April 9, 1998. Revision received May 21, 1998.
Michigan Math. J. 46 (1999).
251
252 Tim Hsu & Daniel T. Wise
In particular, if G
v
∼
=
Z for all v ∈
0
then G
v
is called a graph group or
right-angled Artin group. If G
v
∼
=
Z/2 for all v ∈
0
then G
v
is a Coxeter group
with all edges labeled either 2 or ∞; such groups are known as right-angled Cox-
eter groups.
Definition 2.2. Let be a finite simplicial graph, and let G
v
and C
v
be two
sets of vertex groups for such that there exists some homomorphism ϕ
v
: G
v
→
C
v
for each v ∈
0
. The natural map from G
v
to C
v
is the unique homomor-
phism that restricts to ϕ
v
on each of the G
v
. (The existence of such a map follows
easily from the definition of graph product.)
Now, by definition, any element g of a graph product G
v
can be represented
as a product g
1
g
2
...g
n
, where each g
i
is an element of some vertex group G
v
.
Definition 2.3, Definition 2.4, and Theorem 2.5 describe howto do so in the “short-
est” possible way.
Definition 2.3. If g is an element of a graph product G
v
, then we may repre-
sent g by a product W = g
1
g
2
...g
n
of elements g
i
, each of which is an element
of some vertex group G
v
.Wis called a word representing g, and the g
i
are called
the syllables of W. The number of syllables in W is called the length of W.
Note that each of the following “moves” changes a given word W to a word W
0
that represents the same element of G
v
as W does and has length less than or
equal to the length of W.
1. Remove a syllable g
i
= 1.
2. Replace consecutive syllables g
i
and g
i+1
in the same vertex group G
v
with the
single syllable (g
i
g
i+1
).
3. For consecutive syllables g
i
∈ G
v
and g
i+1
∈ G
w
such that [v, w] ∈
1
, ex-
change g
i
and g
i+1
.
Definition 2.4. If g is represented by a word W that cannot be changed to a
shorter word using any sequence of the moves just listed, then W is said to be a
normal form for g.
We give a geometric proof of the following theorem of Green [7] in Section 4. For
the moment, we will be content just to quote it.
Theorem 2.5. A normal form in a graph product represents the trivial element
if and only if it is the empty word.
Finally, we need the following definition.
Definition 2.6. Let and be simplicial graphs, and let G
v
(resp. G
w
) be ver-
texgroups for (resp. ).Afull inclusion is an inclusion ρ : → of simplicial
graphs such that, for any two vertices u, v ∈ , if [ρ(u), ρ(v)]∈
1
then [u, v] ∈
1
. If ρ : → is a full inclusion and G
v
∼
=
G
ρ(v)
for all v ∈
0
, then G
v
is

On Linear and Residual Properties of Graph Products 253
called a full subgroup of G
w
. Note that G
v
is indeed a subgroup of G
w
, since
the homomorphism induced by ρ maps normal forms to normal forms.
3. Graph Products of Coxeter Subgroups
Definition 3.1. By a Coxeter subgroup we mean a subgroupof a Coxeter group.
For example, any finite group G is a Coxeter subgroup, since G is a subgroup of
some symmetric group; and any (possibly infinite) cyclic group G is a Coxeter
subgroup, since G is a subgroup of some (possibly infinite) dihedral group. Note
that since Coxeter groups are linear (subgroups of GL
n
(R)) and residually finite,
so are Coxeter subgroups.
Theorem 3.2. The graph product of Coxeter subgroups is a Coxeter subgroup.
Proof. Let G
v
be a graph product such that, for each v ∈
0
,G
v
is a subgroup
of the Coxeter group C
v
with reflection generators {r
vi
}. Consider the Coxeter
group C with reflection generators {r
vi
}, where v runs over all v ∈
0
, and Cox-
eter relations
order(r
vi
r
wj
) =
order(r
vi
r
vj
) in C
v
for v = w,
2 for v 6= w, [v, w] ∈
1
,
∞ for v 6= w, [v, w] /∈
1
.
(2)
By the definition of graph product, C is the graph product C
v
. Since the natural
map from G
v
to C
v
sends normal forms to normal forms, the theorem follows.
Remark 3.3. Note that Droms and Servatius [6] used a similar construction, in
the special case of a graph product of infinite cyclic groups, to show that the Cay-
ley graphs of graph groups are isomorphic (as undirected graphs) to the Cayley
graphs of right-angled Coxeter groups. However, their graph isomorphism is not
equivariant and does not come from a group homomorphism, so it is quite differ-
ent from our group embedding.
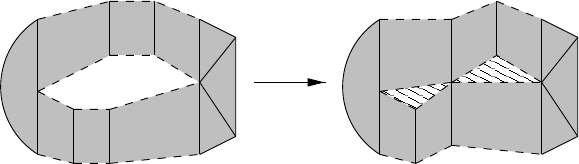
Example 3.4. Let G
v
be the graph group shown on the left-hand side of Fig-
ure 1; or, in other words, let G
v
be the indicated graph product of the infinite
cyclic groups ha
i
i (1 ≤ i ≤ 4). Let C be the Coxeter group whose Coxeter dia-
gram is shown on the right-hand side of Figure 1, using the convention that all
edges are labelled with ∞. Finally, since any infinite cyclic group is a subgroup of
the Coxeter group
∞
•
•, let ϕ be the homomorphism from G
v
to C that embeds
each ha
i
i in the vertical (thick-line)
∞
• • group labelled ha
i
i on the right-hand
side of Figure1. Following the recipe given by (2), we see that ϕ embeds G
v
as a
subgroup of C. (Note that, since graph products and Coxeter groups have opposite
graph conventions for commuting relations, ϕ sends joined vertices to nonjoined
∞
•
• groups, and vice versa.)

254 Tim Hsu & Daniel T. Wise
Figure 1 Embedding a graph group in a Coxeter group.
Theorem 3.2 allows us to conclude that many graph products are Coxeter sub-
groups and thus are linear, residually finite, and so on. For instance, we have the
following corollary.
Corollary 3.5. The graph product of finite groups and cyclic groups is a Cox-
eter subgroup and is therefore linear and residually finite.
In particular, we recover the following result of Humphries [11].
Corollary 3.6. Right-angled Artin groups, or graph groups, are linear.
In fact, we have actually shown that every right-angled Artin group on n genera-
tors is a subgroup of a right-angled Coxeter group on 2n generators.
We may also use Theorem 3.2 (or Corollary 3.5) to obtain a short proof of the
following theorem of Green [7].
Theorem 3.7. The graph product of residually finite groups is residually finite.
Proof. Let G
v
be a graph product, and suppose that each G
v
is residually finite.
We wish to show that, for 1 6= g ∈ G
v
,gsurvives in some finite quotient of
G
v
. Suppose g has some normal form g = g
1
g
2
...g
r
. Choose finite quotients
Q
v
of each of the G
v
such that all of the g
i
survive in their respective quotients.
The natural homomorphism ϕ : G
v
→ Q
v
sends g to an element with a non-
trivial normal form, which means that ϕ(g) 6= 1. Then, since Q
v
is residually
finite (Corollary 3.5), there is some finite quotient of Q
v
in which ϕ(g) survives,
and the theorem follows.
Recall that the profinite topology on a group G is the topology whose closed basis
consists of cosets of finite index subgroups of G. Note that G is residually finite
if and only if {1
G
} is a closed subset and, more generally, a subgroup H of G is
closed if and only if H is the intersection of finite index subgroups of G. Finally,
note that a homomorphism of groups is a continuous map relative to their profinite
topologies. See Higgins [9] for more about the profinite topology.
Green also extended Theorem 3.7 as follows.
Theorem 3.8 (Green). Let G be a graph product of residually finite groups, and
let H be a full subgroup of G. Then H is closed in the profinite topology of G.
We now extend Theorem 3.7 further (Theorem 3.10), using the following lemma.

On Linear and Residual Properties of Graph Products 255
Lemma 3.9. Let G be a residually finite group, and let ϕ : G → G be a retrac-
tion map (i.e., ϕ
2
= ϕ). Then:
(1) ϕ(G) is closed in the profinite topology of G.
(2) Any closed subgroup of ϕ(G) in the profinite topology on ϕ(G) is also closed
as a subgroup of G. In other words, the inclusion map ϕ(G) → G is a ho-
meomorphism with respect to the profinite topologies of the two groups.
Proof. Since H = ϕ(G) is a retract of G, if N = ker ϕ then G = NH and
N ∩ H = 1. Using the residual finiteness of G, let G
i
be a sequence of finite in-
dex normal subgroups of G whose intersection is 1, and let N
i
= N ∩ G
i
. Then,
since
[G : N
i
H ] = [NH : N
i
H ] = [N : N
i
] ≤ [G : G
i
], (3)
it follows that N
i
H is a sequence of finite index subgroups of G. However, since
any element of G is uniquely expressed as a product nh (n ∈ N, h ∈ H),the in-
tersection of the N
i
H is precisely H. Statement (1) follows.
As for (2), let K denote the subgroup ϕ(G) equipped with its own profinite
topology, and let L be a closed subgroup of K. Since the homomorphism ϕ : G →
K is continuous, ϕ
−1
(L) is thepreimageof a closed set of K and is therefore closed
in G. Then, since L is the intersection of the closed subgroups K and ϕ
−1
(L) of
G, L must also be closed in G. The lemma follows.
Theorem 3.10 (Green). Let be a full subgraph of (Definition 2.6), and for
v ∈
0
let G
v
be residually finite. Then the inclusion of G
v
as a full subgroup
of G
v
is a homeomorphism with respect to the profinite topologies of the two
groups.
Proof. For each v ∈
0
, let ψ
v
: G
v
→ G
v
be the identity if v ∈
0
and trivial
otherwise. Then the resulting natural map ϕ is a retraction from G
v
onto G
v
,
and the theorem follows from Lemma 3.9.
Remark 3.11. In a future paper [10], we will provide a more extensive answer to
the question of which subgroups of a graph group G
v
are closed. Specifically,
we hope to show that any subgroup of G
v
that has finitely generated intersection
with every conjugate of every full subgroup of G
v
is closed in G
v
.
4. Proof of the Normal Form Theorem
In this section we give a proof of Theorem 2.5 based on the geometry of van Kam-
pen diagrams. Throughout this section, we fix a graph product G
v
and use the
presentation of G
v
obtained by combining the “multiplication table” presenta-
tions of the G
v
and the commutators in (1), Definition 2.1. Relators of the first
type we call multiplication relators, and relators of the second type we call graph
relators.
Throughout this section, we consider a word W (Definition 2.3) that represents
the trivial element of G
v
and a van Kampen diagram D for W. That is, following
256 Tim Hsu & Daniel T. Wise
Lyndon and Schupp [12], we consider a singular disc diagram D (with basepoint
d ∈ ∂D) made by “sticking together” relators from the presentation of G
v
such
that W is the label of a closed path around ∂D beginning and ending at d. (Note
that, because of our chosen basepoint d, there is a well-defined notion of being
“between” two syllables of ∂D.)
Definition 4.1. For v ∈
0
, we define the diagram D
v
to be the disjoint union
of all 2-cells of D that correspond to 2-cells coming either from a multiplication
relator in G
v
or from a graph relator [g
v
,g
w
] (g
v
∈ G
v
), identifying two 2-cells
along an edge e if and only if their images in D intersect along e.
Definition 4.2. We define a v-component of D to be a component of D
v
. For a
v-component C, we define ∂
∗
C (the “outer boundary” of C)to be the set of edges
of ∂C which are mapped to ∂D and which also correspond to elements of G
v
.
Figure 2 A v-component mapped into D.
Note that a v-component C is not necessarily a subdiagram of D, since extra
identifications may occur in D along 0-cells of C. Figure 2 gives an example of a
v-component that has suchextra identifications whenmappedinto D. (Solid edges
correspond to elements of G
v
, and dashed edges correspond to other elements.)
Note also that, for a v-component C, ∂
∗
C may be a disconnected, proper subset
of ∂C. Nevertheless, since the cyclic ordering on ∂D determines a cyclic ordering
of the edges of ∂
∗
C, by concatenating the edges of ∂
∗
C we obtain a closed directed
path ∂
B
C (the “closed outer boundary” of C). Now, since each of the edges of ∂
B
C
is labelled by an element of G
v
,∂
B
C represents a conjugacy class of G
v
. We can
therefore state the following key lemma.
Lemma 4.3. If C is a v-component, then ∂
B
C represents the trivial element of G
v
.
Proof. Let q be the map defined by quotienting each of the 2-cells of C of the
form [g
v
,g
w
] to a 1-cell g
v
or, in other words, by retracting each graph relator
[g
v
,g
w
] along its two g
w
sides. It is easy to see that the resulting quotient q(C) is
a diagram made by sticking together multiplication relators from G
v
. Therefore,
it is enough to show that all of the edges in the boundary of q(C) come from edges
in ∂
∗
C, for then ∂(q(C)) has one component, q(C) is a van Kampen diagram in
the presentation of G
v
, and ∂(q(C)) = ∂
∗
C. (Note that the cyclic ordering of the

On Linear and Residual Properties of Graph Products 257
Figure 3 Are there boundary edges on the inside of D?
edges of ∂
∗
C determined by ∂D is the same as the cyclic ordering of these edges
in ∂(q(C )).)
Now, if there is some edge e in the boundary of q(C) such that q
−1
(e) ∩ ∂
∗
C =
∅, then q
−1
(e) must include some edge e
0
such that the image of e
0
in D is on the
boundary of the image of C and also on the inside of D, as shown by the heavy
edges in Figure 3. However, since any edge on the inside of D corresponding to
an element of G
v
must border a 2-cell coming either from a multiplication relator
of G
v
or from a graph relator [g
v
,g
w
] (g
v
∈ G
v
) on both sides, no such edge e
0
exists. The lemma follows.
Proof of Theorem 2.5. Let W be a word that represents the trivial element of G
v
.
First, reduce W as much as possible by moves of type 1 and 2 (see the list before
Definition 2.4). If C
v
is a v-component then it follows—because ∂
B
C
v
= 1inG
v
(Lemma 4.3) and W cannot be further reduced by moves of type1and 2—that the
image of ∂
∗
C
v
in D is not connected. We may therefore choose some v ∈
0
and
some v-component C
v
with syllables g
v
,g
0
v
∈ ∂
∗
C
v
such that g
v
and g
0
v
are inner-
most, that is, such that there is no syllable from ∂
∗
C
v
between g
v
and g
0
v
, and there
is no w-component C
w
such that ∂
∗
C
w
contains syllables g
w
and g
0
w
both between
g
v
and g
0
v
.
g
w
g
v
’
g
v
d
Figure 4 Other components must pass through C
v
.

258 Tim Hsu & Daniel T. Wise
Now let g
w
be a syllable between g
v
and g
0
v
, and let C
w
be the w-component
containing g
w
. As before, since ∂
B
C
w
= 1inG
w
,∂
∗
C
w
must have at least two
components. Furthermore, only one component of ∂
∗
C
w
can be between g
v
and
g
0
v
, since g
v
and g
0
v
are innermost. The image of C
w
must therefore intersect the
image of C
v
at a 2-cell (see Figure 4), which implies that [v, w] ∈
1
. In other
words, for all syllables g
w
between g
v
and g
0
v
, we see that g
w
commutes with g
v
.
Therefore, using moves of type 3, we may change W to a word W
0
= ...g
v
g
0
v
...
and then, using a move of type 2, we may make W
0
shorter. The theorem follows
by induction on the length of W.
5. Problems
In closing, we raise two questions.
1. Is the finite graph product of finitely generated linear groups linear? Clearly
the direct product of linear groups is linear, and it is also known that the free prod-
uct of linear groups is linear (Wehrfritz [14]).
2. Are Artin groups linear? Are they residually finite? Note that a special case
of the first question is the long-standing open question of whether braid groups
are linear. Also, an affirmative answer to either of these questions would produce
a solution to the word problem for Artin groups. More speculatively, we ask: Are
Artin groups Coxeter subgroups?
References
[1] A. Baudisch, Subgroups of semifree groups, Ph.D. thesis, Akademie der Wis-
senschaften der DDR Zentralinstitut for Mathematik und Mechanik, 1979.
[2] M. Bestvina and N. Brady, Morse theory and finiteness properties of groups,
Invent. Math. 129 (1997), 445–470.
[3] C. Droms, Isomorphisms of graph groups, Proc. Amer. Math. Soc. 100 (1987),
407–408.
[4]
, Subgroups of graph groups, J. Algebra 110 (1987), 519–522.
[5] C. Droms, B. Servatius, and H. Servatius, The finite basis extension property
and graph groups, Topology and combinatorial group theory (Hanover, NH,
1986/1987; Enfield, NH, 1988), Lecture Notes in Math., 1440, pp. 52–58,
Springer-Verlag, Berlin, 1990.
[6] C. Droms and H. Servatius, The Cayley graphs of Coxeter and Artin groups,
Proc. Amer. Math. Soc. 118 (1993), 693–698.
[7] E. Green, Graph products, Ph.D. thesis, Univ. of Warwick, 1991.
[8] S. Hermiller and J. Meier, Algorithms and geometry for graph products of
groups, J. Algebra 171 (1995), 230–257.
[9] P. J. Higgins, An introduction to topological groups, London Math. Soc. Lecture
Note Ser., 15, Cambridge University Press, 1974.
[10] T. Hsu and D. Wise, Subgroup separability of graph groups (in preparation).
[11] S. P. Humphries, On representations of Artin groups and the Tits conjecture,
J. Algebra 169 (1994), 847–862.
[12] R. Lyndon and P. Schupp, Combinatorial group theory, Springer-Verlag, New
York, 1977.
On Linear and Residual Properties of Graph Products 259
[13] L. VanWyk, Graph groups are biautomatic, J. Pure Appl. Algebra 94 (1994),
341–352.
[14] B. A. F. Wehrfritz, Generalized free products of linear groups, Proc. London
Math. Soc. (3) 27 (1973), 402–424.
T. Hsu D. T. Wise
Department of Mathematics Department of Mathematics
Pomona College Cornell University
Claremont, CA 91711 Ithaca, NY 14853
[email protected].edu daniwise@math.cornell.edu
