95057_01_ch01_p001-066.qxd

hen writer Lewis Carroll took Alice

on her journeys down the rabbit hole to

Wonderland and through the looking

glass, she had many fantastic

encounters with the tea-sipping Mad

Hatter, a hookah-smoking Caterpillar, the

White Rabbit, the Cheshire Cat, the Red

and White Queens, and Tweedledum and

Tweedledee. On the surface, Carroll’s

writings seem to be delightful nonsense

and mere children’s entertainment. Many

people are quite surprised to learn that

Alice’s Adventures in Wonderland is as

much an exercise in logic as it is a fantasy

and that Lewis Carroll was actually

Charles Dodgson, an Oxford

mathematician. Dodgson’s many writings

include the whimsical The Game of Logic

and the brilliant Symbolic Logic, in

addition to Alice’s Adventures in

Wonderland and Through the Looking

Glass.

WHAT WE WILL DO In This Chapter

WE’LL EXPLORE DIFFERENT TYPES OF LOGIC OR

REASONING:

• Deductive reasoning involves the application of a

general statement to a speciﬁc case; this type of

logic is typiﬁed in the classic arguments of the

renowned Greek logician Aristotle.

• Inductive reasoning involves generalizing after a

pattern has been recognized and established; this

type of logic is used in the solving of puzzles.

WE’LL ANALYZE AND EXPLORE VARIOUS TYPES

OF STATEMENTS AND THE CONDITIONS UNDER

WHICH THEY ARE TRUE:

• A statement is a simple sentence that is either true

or false. Simple statements can be connected to

form compound, or more complicated, statements.

• Symbolic representations reduce a compound

statement to its basic form; phrases that appear to

be different may actually have the same basic

structure and meaning.

continued

Logic

continued

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 1

Property

and White Queens, and Tweedledum and

Property

and White Queens, and Tweedledum and

Tweedledee. On the surface, Carroll’s

Property

Tweedledee. On the surface, Carroll’s

writings seem to be delightful nonsense

Property

writings seem to be delightful nonsense

and mere children’s entertainment. Many

Property

and mere children’s entertainment. Many

people are quite surprised to learn that

Property

people are quite surprised to learn that

Alice’s Adventures in Wonderland

Property

Alice’s Adventures in Wonderland

much an exercise in logic as it is a fantasy

Property

much an exercise in logic as it is a fantasy

and that Lewis Carroll was actually

Property

and that Lewis Carroll was actually

Charles Dodgson, an Oxford

Property

Charles Dodgson, an Oxford

Hatter, a hookah-smoking Caterpillar, the

White Rabbit, the Cheshire Cat, the Red

and White Queens, and Tweedledum and

Tweedledee. On the surface, Carroll’s

Cengage

Hatter, a hookah-smoking Caterpillar, the

Cengage

Hatter, a hookah-smoking Caterpillar, the

Cengage

Learning

WHAT WE WILL DO In This Chapter — continued

WE’LL ANALYZE AND EXPLORE CONDITIONAL, OR “IF . . . THEN . . .,”

STATEMENTS:

• In everyday conversation, we often connect phrases by saying “if this, then

that.” However, does “this” actually guarantee “that”? Is “this” in fact

necessary for “that”?

• How does “if” compare with “only if”? What does “if and only if” really

mean?

WE’LL DETERMINE THE VALIDITY OF AN ARGUMENT:

• What constitutes a valid argument? Can a valid argument yield a false

conclusion?

• You may have used Venn diagrams to depict a solution set in an algebra

class. We will use Venn diagrams to visualize and analyze an argument.

• Some of Lewis Carroll’s whimsical arguments are valid, and some are not.

How can you tell?

Webster’s New World College Dictionary deﬁnes logic as “the

science of correct reasoning; science which describes relationships among

propositions in terms of implication, contradiction, contrariety, conversion,

etc.” In addition to being ﬂaunted in Mr. Spock’s claim that “your human

emotions have drawn you to an illogical conclusion” and in Sherlock

Holmes’s immortal phrase “elementary, my dear Watson,” logic is

fundamental both to critical thinking and to problem solving. In today’s

world of misleading commercial claims, innuendo, and political rhetoric,

the ability to distinguish between valid and invalid arguments is

important.

In this chapter, we will study the basic components of logic and its

application. Mischievous, wild-eyed residents of Wonderland, eccentric,

violin-playing detectives, and cold, emotionless Vulcans are not the only

ones who can beneﬁt from logic. Armed with the fundamentals of logic, we

can surely join Spock and “live long and prosper!”

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 2

Property

emotions have drawn you to an illogical conclusion” and in Sherlock

Property

emotions have drawn you to an illogical conclusion” and in Sherlock

Holmes’s immortal phrase “elementary, my dear Watson,” logic is

Property

Holmes’s immortal phrase “elementary, my dear Watson,” logic is

fundamental both to critical thinking and to problem solving. In today’s

Property

fundamental both to critical thinking and to problem solving. In today’s

world of misleading commercial claims, innuendo, and political rhetoric,

Property

world of misleading commercial claims, innuendo, and political rhetoric,

the ability to distinguish between valid and invalid arguments is

Property

the ability to distinguish between valid and invalid arguments is

important.

Property

important.

application. Mischievous, wild-eyed residents of Wonderland, eccentric,

Property

application. Mischievous, wild-eyed residents of Wonderland, eccentric,

propositions in terms of implication, contradiction, contrariety, conversion,

etc.” In addition to being ﬂaunted in Mr. Spock’s claim that “your human

emotions have drawn you to an illogical conclusion” and in Sherlock

Holmes’s immortal phrase “elementary, my dear Watson,” logic is

Cengage

Webster’s New World College Dictionary

Cengage

Webster’s New World College Dictionary

science of correct reasoning; science which describes relationships among

Cengage

science of correct reasoning; science which describes relationships among

propositions in terms of implication, contradiction, contrariety, conversion,

Cengage

propositions in terms of implication, contradiction, contrariety, conversion,

etc.” In addition to being ﬂaunted in Mr. Spock’s claim that “your human

Cengage

etc.” In addition to being ﬂaunted in Mr. Spock’s claim that “your human

Cengage

Learning

Can a valid argument yield a false

Learning

Can a valid argument yield a false

• You may have used Venn diagrams to depict a solution set in an algebra

Learning

• You may have used Venn diagrams to depict a solution set in an algebra

class. We will use Venn diagrams to visualize and analyze an argument.

Learning

class. We will use Venn diagrams to visualize and analyze an argument.

• Some of Lewis Carroll’s whimsical arguments are valid, and some are not.

Learning

• Some of Lewis Carroll’s whimsical arguments are valid, and some are not.

1.1 Deductive versus Inductive Reasoning 3

Logic is the science of correct reasoning.

Auguste Rodin captured this ideal in his

bronze sculpture The Thinker.

In their quest for logical perfection, the

Vulcans of Star Trek abandoned all emotion.

Mr. Spock’s frequent proclamation that

“emotions are illogical” typiﬁed this attitude.

Vanni/Art Resource, NY

PARAMOUNT TELEVISION/THE KOBAL COLLECTION

1.1 Deductive versus Inductive Reasoning

bjectives

•

Use Venn diagrams to determine the validity of deductive arguments

•

Use inductive reasoning to predict patterns

Logic is the science of correct reasoning. Webster’s New World College Dictionary

deﬁnes reasoning as “the drawing of inferences or conclusions from known or

assumed facts.” Reasoning is an integral part of our daily lives; we take appropriate

actions based on our perceptions and experiences. For instance, if the sky is heav-

ily overcast this morning, you might assume that it will rain today and take your

umbrella when you leave the house.

Problem Solving

Logic and reasoning are associated with the phrases problem solving and critical

thinking. If we are faced with a problem, puzzle, or dilemma, we attempt to reason

through it in hopes of arriving at a solution.

The ﬁrst step in solving any problem is to deﬁne the problem in a thorough

and accurate manner. Although this might sound like an obvious step, it is often

overlooked. Always ask yourself, “What am I being asked to do?” Before you can

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 3

Property

bjectives

Property

bjectives

Use Venn diagrams to determine the validity of deductive arguments

Property

Use Venn diagrams to determine the validity of deductive arguments

Use inductive reasoning to predict patterns

Property

Use inductive reasoning to predict patterns

Cengage

Deductive versus Inductive Reasoning

Cengage

Deductive versus Inductive Reasoning

Learning

In their quest for logical perfection, the

Learning

In their quest for logical perfection, the

Vulcans of

Learning

Vulcans of

Mr. Spock’s frequent proclamation that

Learning

Mr. Spock’s frequent proclamation that

“emotions are illogical” typiﬁed this attitude.

Learning

“emotions are illogical” typiﬁed this attitude.

solve a problem, you must understand the question. Once the problem has been

deﬁned, all known information that is relevant to it must be gathered, organized,

and analyzed. This analysis should include a comparison of the present problem to

previous ones. How is it similar? How is it different? Does a previous method of

solution apply? If it seems appropriate, draw a picture of the problem; visual

representations often provide insight into the interpretation of clues.

Before using any speciﬁc formula or method of solution, determine whether

its use is valid for the situation at hand. A common error is to use a formula or

method of solution when it does not apply. If a past formula or method of solution

is appropriate, use it; if not, explore standard options and develop creative alterna-

tives. Do not be afraid to try something different or out of the ordinary. “What if I

try this . . . ?” may lead to a unique solution.

Deductive Reasoning

Once a problem has been deﬁned and analyzed, it might fall into a known category

of problems, so a common method of solution may be applied. For instance, when

one is asked to solve the equation x

 2x  1, realizing that it is a second-degree

equation (that is, a quadratic equation) leads one to put it into the standard

form (x

 2x  1  0) and apply the Quadratic Formula.

EXAMPLE 1 USING DEDUCTIVE REASONING TO SOLVE AN EQUATION Solve the

equation x

 2x  1.

SOLUTION The given equation is a second-degree equation in one variable. We know that all

second-degree equations in one variable (in the form ax

 bx  c  0) can be

solved by applying the Quadratic Formula:

x 

b ; 2b

 4ac

4 CHAPTER 1 Logic

Using his extraordinary powers of logical deduction, Sherlock Holmes

solves another mystery. “Finding the villain was elementary, my dear

Watson.”

AVCO EMBASSY/THE KOBAL COLLECTION

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 4

Property

tives. Do not be

Property

tives. Do not be

try this . . . ?” may lead to a unique solution.

Property

try this . . . ?” may lead to a unique solution.

Deductive Reasoning

Property

Deductive Reasoning

method of solution when it does not apply. If a past formula or method of solution

is appropriate, use it; if not, explore standard options and develop creative alterna-

tives. Do not be

afraid to try something different or out of the ordinary. “What if I

try this . . . ?” may lead to a unique solution.

Cengage

solve a problem, you must understand the question. Once the problem has been

Cengage

solve a problem, you must understand the question. Once the problem has been

deﬁned, all known information that is relevant to it must be gathered, organized,

Cengage

deﬁned, all known information that is relevant to it must be gathered, organized,

and analyzed. This analysis should include a comparison of the present problem to

Cengage

and analyzed. This analysis should include a comparison of the present problem to

previous ones. How is it similar? How is it different? Does a previous method of

Cengage

previous ones. How is it similar? How is it different? Does a previous method of

solution apply? If it seems appropriate, draw a picture of the problem; visual

Cengage

solution apply? If it seems appropriate, draw a picture of the problem; visual

representations often provide insight into the interpretation of clues.

Cengage

representations often provide insight into the interpretation of clues.

Before using any speciﬁc formula or method of solution, determine whether

Cengage

Before using any speciﬁc formula or method of solution, determine whether

its use is valid for the situation at hand. A common error is to use a formula or

Cengage

its use is valid for the situation at hand. A common error is to use a formula or

method of solution when it does not apply. If a past formula or method of solution

Cengage

method of solution when it does not apply. If a past formula or method of solution

is appropriate, use it; if not, explore standard options and develop creative alterna-

Cengage

is appropriate, use it; if not, explore standard options and develop creative alterna-

Learning

Using his extraordinary powers of logical deduction, Sherlock

Learning

Using his extraordinary powers of logical deduction, Sherlock

Holmes

Learning

Holmes

solves another mystery. “Finding the villain was elementary,

Learning

solves another mystery. “Finding the villain was elementary,

my dear

Learning

my dear

AVCO EMBASSY/THE KOBAL COLLECTION

Learning

AVCO EMBASSY/THE KOBAL COLLECTION

Therefore, x

 2x  1 can be solved by applying the Quadratic Formula:

The solutions are

In Example 1, we applied a general rule to a speciﬁc case; we reasoned that

it was valid to apply the (general) Quadratic Formula to the (speciﬁc) equation

 2x  1. This type of logic is known as deductive reasoning—that is, the

application of a general statement to a speciﬁc instance.

Deductive reasoning and the formal structure of logic have been studied for

thousands of years. One of the earliest logicians, and one of the most renowned,

was Aristotle (384–322

B.C.). He was the student of the great philosopher Plato and

the tutor of Alexander the Great, the conqueror of all the land from Greece to

India. Aristotle’s philosophy is pervasive; it inﬂuenced Roman Catholic theology

through St. Thomas Aquinas and continues to inﬂuence modern philosophy. For

centuries, Aristotelian logic was part of the education of lawyers and politicians

and was used to distinguish valid arguments from invalid ones.

For Aristotle, logic was the necessary tool for any inquiry, and the syllogism

was the sequence followed by all logical thought. Asyllogism is an argument com-

posed of two statements, or premises (the major and minor premises), followed by

a conclusion. For any given set of premises, if the conclusion of an argument is

guaranteed (that is, if it is inescapable in all instances), the argument is valid. If the

conclusion is not guaranteed (that is, if there is at least one instance in which it

does not follow), the argument is invalid.

Perhaps the best known of Aristotle’s syllogisms is the following:

1. All men are mortal. major premise

2. Socrates is a man. minor premise

Therefore, Socrates is mortal. conclusion

When the major premise is applied to the minor premise, the conclusion is

inescapable; the argument is valid.

Notice that the deductive reasoning used in the analysis of Example 1 has

exactly the same structure as Aristotle’s syllogism concerning Socrates:

1. All second-degree equations in one variable can be major premise

solved by applying the Quadratic Formula.

2. x

 2x  1 is a second-degree equation in one variable. minor premise

Therefore, x

 2x  1 can be solved by applying the conclusion

Quadratic Formula.

x  1  22

and x  1  22.

x  1 ; 22

x 

211 ; 22

x 

2 ; 222

x 

2 ; 28

x 

2 ; 24  4

x 

122 ; 2122

 1421112

2112

 2x  1  0

 2x  1

1.1 Deductive versus Inductive Reasoning 5

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 5

Property

centuries, Aristotelian logic was part of the education of lawyers and politicians

Property

centuries, Aristotelian logic was part of the education of lawyers and politicians

and was used to distinguish valid arguments from invalid ones.

Property

and was used to distinguish valid arguments from invalid ones.

For Aristotle, logic was the necessary tool for any inquiry, and the syllogism

Property

For Aristotle, logic was the necessary tool for any inquiry, and the syllogism

was the sequence followed by all logical thought. A

Property

was the sequence followed by all logical thought. A

posed of two statements, or

Property

posed of two statements, or

the tutor of Alexander the Great, the conqueror of all the land from Greece to

India. Aristotle’s philosophy is pervasive; it inﬂuenced Roman Catholic theology

through St. Thomas Aquinas and continues to inﬂuence modern philosophy. For

centuries, Aristotelian logic was part of the education of lawyers and politicians

Cengage

In Example 1, we applied a general rule to a speciﬁc case; we reasoned that

Cengage

In Example 1, we applied a general rule to a speciﬁc case; we reasoned that

it was valid to apply the (general) Quadratic Formula to the (speciﬁc) equation

Cengage

it was valid to apply the (general) Quadratic Formula to the (speciﬁc) equation

1. This type of logic is known as

Cengage

1. This type of logic is known as

application of a general statement to a speciﬁc instance.

Cengage

application of a general statement to a speciﬁc instance.

Deductive reasoning and the formal structure of logic have been studied for

Cengage

Deductive reasoning and the formal structure of logic have been studied for

thousands of years. One of the earliest logicians, and one of the most renowned,

Cengage

thousands of years. One of the earliest logicians, and one of the most renowned,

was Aristotle (384–322

Cengage

was Aristotle (384–322

the tutor of Alexander the Great, the conqueror of all the land from Greece to

Cengage

the tutor of Alexander the Great, the conqueror of all the land from Greece to

India. Aristotle’s philosophy is pervasive; it inﬂuenced Roman Catholic theology

Cengage

India. Aristotle’s philosophy is pervasive; it inﬂuenced Roman Catholic theology

Learning

and

Learning

and

Learning



Learning



Learning



Learning



6 CHAPTER 1 Logic

Each of these syllogisms is of the following general form:

1. If A, then B. All A are B. (major premise)

2. x is A. We have A. (minor premise)

Therefore, x is B. Therefore, we have B. (conclusion)

Historically, this valid pattern of deductive reasoning is known as modus ponens.

Deductive Reasoning and Venn Diagrams

The validity of a deductive argument can be shown by use of a Venn diagram. A

Venn diagram is a diagram consisting of various overlapping ﬁgures contained

within a rectangle (called the “universe”). To depict a statement of the form “All

A are B” (or, equivalently, “If A, then B”), we draw two circles, one inside the

other; the inner circle represents A, and the outer circle represents B. This rela-

tionship is shown in Figure 1.1.

Venn diagrams depicting “No A are B” and “Some A are B” are shown in Fig-

ures 1.2 and 1.3, respectively.

All A are B. (If A, then B.)

FIGURE 1.1

No A are B.

FIGURE 1.2

Some A are B. (At least one A is B.)FIGURE 1.3

EXAMPLE 2 ANALYZING A DEDUCTIVE ARGUMENT Construct a Venn diagram to

verify the validity of the following argument:

1. All men are mortal.

2. Socrates is a man.

Therefore, Socrates is mortal.

SOLUTION Premise 1 is of the form “All A are B” and can be represented by a diagram like that

shown in Figure 1.4.

Premise 2 refers to a speciﬁc man, namely, Socrates. If we let x  Socrates,

the statement “Socrates is a man” can then be represented by placing x within the

circle labeled “men,” as shown in Figure 1.5. Because we placed x within the

“men” circle, and all of the “men” circle is inside the “mortal” circle, the conclu-

sion “Socrates is mortal” is inescapable; the argument is valid.

men

mortal

men

mortal

x  Socrates

All men are mortal.

FIGURE 1.4

Socrates is mortal.FIGURE 1.5

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 6

Property

verify the validity of the following argument:

Property

verify the validity of the following argument:

1. All men are mortal.

Property

1. All men are mortal.

2. Socrates is a man.

Property

2. Socrates is a man.

Property

Therefore, Socrates is mortal.

Property

Therefore, Socrates is mortal.

Premise 1 is of the form “All

Property

Premise 1 is of the form “All

shown in Figure 1.4.

Property

shown in Figure 1.4.

Property

SOLUTION

Property

SOLUTION

Property

ANALYZING A DEDUCTIVE ARGUMENT

verify the validity of the following argument:

1. All men are mortal.

Cengage

are

Cengage

are

Cengage

ANALYZING A DEDUCTIVE ARGUMENT

Cengage

ANALYZING A DEDUCTIVE ARGUMENT

Learning

within a rectangle (called the “universe”). To depict a statement of the form “All

Learning

within a rectangle (called the “universe”). To depict a statement of the form “All

”), we draw two circles, one inside the

Learning

”), we draw two circles, one inside the

and the outer circle represents

Learning

and the outer circle represents

Learning

” and “Some

Learning

” and “Some

Learning

are

Learning

are

Learning

” are shown in Fig-

Learning

” are shown in Fig-

Learning

1.1 Deductive versus Inductive Reasoning 7

supervise the educa-

tion of his son

Alexander, the future

Alexander the Great.

Aristotle accepted

the invitation and

taught Alexander

until he succeeded

his father as ruler. At

that time, Aristotle

founded a school

known as the

Lyceum, or Peripatetic School. The school

had a large library with many maps, as

well as botanical gardens containing an

extensive collection of plants and animals.

Aristotle and his students would walk

about the grounds of the Lyceum while dis-

cussing various subjects (peripatetic is

from the Greek word meaning “to walk”).

Many consider Aristotle to be a

founding father of the study of biology

and of science in general; he observed

and classiﬁed the behavior and

anatomy of hundreds of living creatures.

Alexander the Great, during his many

military campaigns, had his troops

gather specimens from distant places for

Aristotle to study.

Aristotle was a proliﬁc writer; some

historians credit him with the writing of

over 1,000 books. Most of his works

have been lost or destroyed, but schol-

ars have recreated some of his more in-

ﬂuential works, including Organon.

Historical

Note

Aristotle’s collective works on syllogisms and

deductive logic are known as Organon,

meaning “instrument,” for logic is the instrument

used in the acquisition of knowledge.

Collections of the New York Public Library

ristotle was born in

384

B.C. in the small

Macedonian town of Stagira,

200 miles north of Athens, on

the shore of the Aegean

Sea. Aristotle’s father was the

personal physician of King

Amyntas II, ruler of Macedo-

nia. When he was seventeen,

Aristotle enrolled at the Academy in

Athens and became a student of the

famed Plato.

Aristotle was one of Plato’s brightest

students; he frequently questioned Plato’s

teachings and openly disagreed with

him. Whereas Plato emphasized the

study of abstract ideas and mathematical

truth, Aristotle was more interested in

observing the “real world” around him.

Plato often referred to Aristotle as “the

brain” or “the mind of the school.” Plato

commented, “Where others need the

spur, Aristotle needs the rein.”

Aristotle stayed at the Academy for

twenty years, until the death of Plato. Then

the king of Macedonia invited Aristotle to

Museo Archaeologico Nazionale, Naples,

EXAMPLE 3 ANALYZING A DEDUCTIVE ARGUMENT Construct a Venn diagram to

determine the validity of the following argument:

1. All doctors are men.

2. My mother is a doctor.

Therefore, my mother is a man.

SOLUTION Premise 1 is of the form “All A are B”; the argument is depicted in Figure 1.6.

No matter where x is placed within the “doctors” circle, the conclusion “My

mother is a man” is inescapable; the argument is valid.

Saying that an argument is valid does not mean that the conclusion is true.

The argument given in Example 3 is valid, but the conclusion is false. One’s

mother cannot be a man! Validity and truth do not mean the same thing. An argu-

ment is valid if the conclusion is inescapable, given the premises. Nothing is said

about the truth of the premises. Thus, when examining the validity of an argument,

we are not determining whether the conclusion is true or false. Saying that an

argument is valid merely means that, given the premises, the reasoning used to

obtain the conclusion is logical. However, if the premises of a valid argument are

true, then the conclusion will also be true.

doctors

men

x  My mother

My mother is a man.

FIGURE 1.6

ARISTOTLE 384–322 B.C.

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 7

Property

EXAMPLE

Property

EXAMPLE

Property

ANALYZING A DEDUCTIVE ARGUMENT

Property

ANALYZING A DEDUCTIVE ARGUMENT

Property

gather specimens from distant places for

Aristotle to study.

Cengage

about the grounds of the Lyceum while dis-

Cengage

about the grounds of the Lyceum while dis-

cussing various subjects (

Cengage

cussing various subjects (

peripatetic

Cengage

peripatetic

from the Greek word meaning “to walk”).

Cengage

from the Greek word meaning “to walk”).

Many consider Aristotle to be a

Cengage

Many consider Aristotle to be a

founding father of the study of biology

Cengage

founding father of the study of biology

and of science in general; he observed

Cengage

and of science in general; he observed

and classiﬁed the behavior and

Cengage

and classiﬁed the behavior and

anatomy of hundreds of living creatures.

Cengage

anatomy of hundreds of living creatures.

Alexander the Great, during his many

Cengage

Alexander the Great, during his many

military campaigns, had his troops

Cengage

military campaigns, had his troops

gather specimens from distant places for

Cengage

gather specimens from distant places for

Aristotle to study.

Cengage

Aristotle to study.

Learning

well as botanical gardens containing an

Learning

well as botanical gardens containing an

extensive collection of plants and animals.

Learning

extensive collection of plants and animals.

Aristotle and his students would walk

Learning

Aristotle and his students would walk

about the grounds of the Lyceum while dis-

Learning

about the grounds of the Lyceum while dis-

peripatetic

Learning

peripatetic

Learning

If x is placed as in Figure 1.7, the argument would appear to be valid; the ﬁg-

ure supports the conclusion “The Rock is a professional wrestler.” However, the

placement of x in Figure 1.8 does not support the conclusion; given the premises,

we cannot logically deduce that “The Rock is a professional wrestler.” Since the

conclusion is not inescapable, the argument is invalid.

Saying that an argument is invalid does not mean that the conclusion is false.

Example 4 demonstrates that an invalid argument can have a true conclusion; even

though The Rock is a professional wrestler, the argument used to obtain the con-

clusion is invalid. In logic, validity and truth do not have the same meaning.

Validity refers to the process of reasoning used to obtain a conclusion; truth refers

to conformity with fact or experience.

8 CHAPTER 1 Logic

actors

x = The Rock

professional

wrestlers

actors

x = The Rock

professional

wrestlers

FIGURE 1.7

FIGURE 1.8

EXAMPLE 4 ANALYZING A DEDUCTIVE ARGUMENT Construct a Venn diagram to

determine the validity of the following argument:

1. All professional wrestlers are actors.

2. The Rock is an actor.

Therefore, The Rock is a professional wrestler.

SOLUTION Premise 1 is of the form “All A are B”; the “circle of professional wrestlers” is con-

tained within the “circle of actors.” If we let x represent The Rock, premise 2 sim-

ply requires that we place x somewhere within the actor circle; x could be placed

in either of the two locations shown in Figures 1.7 and 1.8.

Even though The Rock is a

professional wrestler, the

argument used to obtain the

conclusion is invalid.

EXAMPLE 5 ANALYZING A DEDUCTIVE ARGUMENT Construct a Venn diagram to

determine the validity of the following argument:

1. Some plants are poisonous.

2. Broccoli is a plant.

Therefore, broccoli is poisonous.

VENN DIAGRAMS AND INVALID ARGUMENTS

To show that an argument is invalid, you must construct a Venn diagram in

which the premises are met yet the conclusion does not necessarily follow.

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 8

Property

Saying that an argument is invalid does not mean that the conclusion is false.

Property

Saying that an argument is invalid does not mean that the conclusion is false.

Example 4 demonstrates that an invalid argument can have a true conclusion; even

Property

Example 4 demonstrates that an invalid argument can have a true conclusion; even

though The Rock is a professional wrestler, the argument used to obtain the con-

Property

though The Rock is a professional wrestler, the argument used to obtain the con-

clusion is invalid. In logic, validity and truth do not have the same meaning.

Property

clusion is invalid. In logic, validity and truth do not have the same meaning.

Validity

Property

Validity

to conformity with fact or experience.

Property

to conformity with fact or experience.

Property

in Figure 1.8 does not support the conclusion; given the premises,

logically

conclusion is

not

inescapable, the argument is invalid.

Cengage

is placed as in Figure 1.7, the argument would appear to be valid; the ﬁg-

Cengage

is placed as in Figure 1.7, the argument would appear to be valid; the ﬁg-

ure supports the conclusion “The Rock is a professional wrestler.” However, the

Cengage

ure supports the conclusion “The Rock is a professional wrestler.” However, the

in Figure 1.8 does not support the conclusion; given the premises,

Cengage

in Figure 1.8 does not support the conclusion; given the premises,

deduce that “The Rock is a professional wrestler.” Since the

Cengage

deduce that “The Rock is a professional wrestler.” Since the

Cengage

FIGURE 1.8

Cengage

FIGURE 1.8

Learning

actors

Learning

actors

Learning

professional

Learning

professional

wrestlers

Learning

wrestlers

1.1 Deductive versus Inductive Reasoning 9

SOLUTION Premise 1 is of the form “Some A are B”; it can be represented by two overlapping

circles (as in Figure 1.3). If we let x represent broccoli, premise 2 requires that we

place x somewhere within the plant circle. If x is placed as in Figure 1.9, the argu-

ment would appear to be valid. However, if x is placed as in Figure 1.10, the con-

clusion does not follow. Because we can construct a Venn diagram in which the

premises are met yet the conclusion does not follow (Figure 1.10), the argument is

invalid.

plants

poison

x = broccoli

plants

poison

x = broccoli

FIGURE 1.9

FIGURE 1.10

When analyzing an argument via a Venn diagram, you might have to draw

three or more circles, as in the next example.

EXAMPLE 6 ANALYZING A DEDUCTIVE ARGUMENT Construct a Venn diagram to

determine the validity of the following argument:

1. No snake is warm-blooded.

2. All mammals are warm-blooded.

Therefore, snakes are not mammals.

SOLUTION Premise 1 is of the form “No A are B”; it is depicted in Figure 1.11. Premise 2 is of

the form “All A are B”; the “mammal circle” must be drawn within the “warm-

blooded circle.” Both premises are depicted in Figure 1.12.

warm-blooded

snakes

mammals

snakes

warm-blooded

x = snake

No snake is warm-blooded.

FIGURE 1.11

All mammals are warm-blooded.FIGURE 1.12

Because we placed x ( snake) within the “snake” circle, and the “snake”

circle is outside the “warm-blooded” circle, x cannot be within the “mammal” circle

(which is inside the “warm-blooded” circle). Given the premises, the conclusion

“Snakes are not mammals” is inescapable; the argument is valid.

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 9

Property

Premise 1 is of the form “No

Property

Premise 1 is of the form “No

the form “All

Property

the form “All

blooded circle.” Both premises are depicted in Figure 1.12.

Property

blooded circle.” Both premises are depicted in Figure 1.12.

Therefore, snakes are not mammals.

Premise 1 is of the form “No

Cengage

When analyzing an argument via a Venn diagram, you might have to draw

Cengage

When analyzing an argument via a Venn diagram, you might have to draw

three or more circles, as in the next example.

Cengage

three or more circles, as in the next example.

ANALYZING A DEDUCTIVE ARGUMENT

Cengage

ANALYZING A DEDUCTIVE ARGUMENT

determine the validity of the following ar

Cengage

determine the validity of the following ar

1. No snake is warm-blooded.

Cengage

1. No snake is warm-blooded.

2. All mammals are warm-blooded.

Cengage

2. All mammals are warm-blooded.

Cengage

Therefore, snakes are not mammals.

Cengage

Therefore, snakes are not mammals.

Learning

poison

Learning

poison

broccoli

Learning

broccoli

Learning

FIGURE 1.10

Learning

FIGURE 1.10

When analyzing an argument via a Venn diagram, you might have to draw

Learning

When analyzing an argument via a Venn diagram, you might have to draw

three or more circles, as in the next example.

Learning

three or more circles, as in the next example.

You might have encountered Venn diagrams when you studied sets in your

algebra class. The academic ﬁelds of set theory and logic are historically inter-

twined; set theory was developed in the late nineteenth century as an aid in the

study of logical arguments. Today, set theory and Venn diagrams are applied to

areas other than the study of logical arguments; we will utilize Venn diagrams in

our general study of set theory in Chapter 2.

Inductive Reasoning

The conclusion of a valid deductive argument (one that goes from general to spe-

ciﬁc) is guaranteed: Given true premises, a true conclusion must follow. However,

there are arguments in which the conclusion is not guaranteed even though the

premises are true. Consider the following:

1. Joe sneezed after petting Frako’s cat.

2. Joe sneezed after petting Paulette’s cat.

Therefore, Joe is allergic to cats.

Is the conclusion guaranteed? If the premises are true, they certainly support the

conclusion, but we cannot say with 100% certainty that Joe is allergic to cats. The

conclusion is not guaranteed. Maybe Joe is allergic to the ﬂea powder that the cat

owners used; maybe he is allergic to the dust that is trapped in the cats’ fur; or

maybe he has a cold!

Reasoning of this type is called inductive reasoning. Inductive reasoning

involvesgoing froma seriesof speciﬁccases toa generalstatement (seeFigure 1.13).

Although it may seem to follow and may in fact be true, the conclusion in an in-

ductive argument is never guaranteed.

10 CHAPTER 1 Logic

general

specific

general

Deductive Reasoning

(Conclusion is guaranteed.)

Inductive Reasoning

(Conclusion may be probable but is

not guaranteed.)

FIGURE 1.13

EXAMPLE 7 INDUCTIVE REASONING AND PATTERN RECOGNITION What is the

next number in the sequence 1, 8, 15, 22, 29, . . . ?

SOLUTION Noticing that the difference between consecutive numbers in the sequence is 7, we

may be tempted to say that the next term is 29  7  36. Is this conclusion guar-

anteed? No! Another sequence in which numbers differ by 7 are dates of a given

day of the week. For instance, the dates of the Saturdays in the year 2011 are

(January) 1, 8, 15, 22, 29, (February) 5, 12, 19, 26, . . . . Therefore, the next num-

ber in the sequence 1, 8, 15, 22, 29, . . . might be 5. Without further information,

we cannot determine the next number in the given sequence. We can only use

inductive reasoning and give one or more possible answers.

95057_01_ch01_p001-066.qxd 9/27/10 9:32 AM Page 10

Property

specific

Property

specific

Property

general

Cengage

conclusion, but we cannot say with 100% certainty that Joe is allergic to cats. The

Cengage

conclusion, but we cannot say with 100% certainty that Joe is allergic to cats. The

guaranteed. Maybe Joe is allergic to the ﬂea powder that the cat

Cengage

guaranteed. Maybe Joe is allergic to the ﬂea powder that the cat

owners used; maybe he is allergic to the dust that is trapped in the cats’ fur; or

Cengage

owners used; maybe he is allergic to the dust that is trapped in the cats’ fur; or

Reasoning of this type is called inductive reasoning.

Cengage

Reasoning of this type is called inductive reasoning.

involvesgoing froma seriesof speciﬁccases toa generalstatement (seeFigure 1.13).

Cengage

involvesgoing froma seriesof speciﬁccases toa generalstatement (seeFigure 1.13).

Although it may seem to follow and may in fact be true,

Cengage

Although it may seem to follow and may in fact be true,

ductive argument is never guaranteed.

Cengage

ductive argument is never guaranteed.

Cengage

Learning

ciﬁc) is guaranteed: Given true premises, a true conclusion must follow. However,

Learning

ciﬁc) is guaranteed: Given true premises, a true conclusion must follow. However,

there are arguments in which the conclusion is not guaranteed even though the

Learning

there are arguments in which the conclusion is not guaranteed even though the

Is the conclusion guaranteed? If the premises are true, they certainly

Learning

Is the conclusion guaranteed? If the premises are true, they certainly

conclusion, but we cannot say with 100% certainty that Joe is allergic to cats. The

Learning

conclusion, but we cannot say with 100% certainty that Joe is allergic to cats. The

guaranteed. Maybe Joe is allergic to the ﬂea powder that the cat

Learning

guaranteed. Maybe Joe is allergic to the ﬂea powder that the cat

EXAMPLE 8 SOLVING A SUDOKU PUZZLE Solve the sudoku puzzle given in Figure 1.15.

1.1 Deductive versus Inductive Reasoning 11

hroughout history, people have al-

ways been attracted to puzzles,

mazes, and brainteasers. Who can

deny the inherent satisfaction of solving

a seemingly unsolvable or perplexing

riddle? A popular new addition to the

world of puzzle solving is sudoku, a

numbers puzzle. Loosely translated

from Japanese, sudoku means “single

number”; a sudoku puzzle simply in-

volves placing the digits 1 through 9 in

a grid containing 9 rows and

9 columns. In addition, the 9 by 9 grid

of squares is subdivided into nine 3 by

3 grids, or “boxes,” as shown in Fig-

ure 1.14.

The rules of sudoku are quite simple:

Each row, each column, and each box

must contain the digits 1 through 9; and

no row, column, or box can contain 2

squares with the same number. Conse-

quently, sudoku does not require any

arithmetic or mathematical skill; sudoku

requires logic only. In solving a puzzle, a

common thought is “What happens if I

put this number here?”

Like crossword puzzles, sudoku puz-

zles are printed daily in many newspa-

pers across the country and around the

world. Web sites containing sudoku puz-

zles and strategies provide an endless

source of new puzzles and help. See

Exercise 62 to ﬁnd links to popular sites.

Topic x

A blank sudoku grid.FIGURE 1.14

SUDOKU:

LOGIC IN THE REAL WORLD

A sudoku puzzle.

FIGURE 1.15

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 11

Property

EXAMPLE

Property

EXAMPLE

Property

FIGURE 1.14

Property

FIGURE 1.14

A blank sudoku grid.

Cengage

Learning

zles are printed

Learning

zles are printed

pers across the country and around the

Learning

pers across the country and around the

world. Web sites containing sudoku puz-

Learning

world. Web sites containing sudoku puz-

zles and strategies provide an endless

Learning

zles and strategies provide an endless

source of new puzzles and help. See

Learning

source of new puzzles and help. See

Exercise 62 to ﬁnd links to popular sites.

Learning

Exercise 62 to ﬁnd links to popular sites.

Learning

12 CHAPTER 1 Logic

123

456

789

123456789

Box numbers and coordinate system in sudoku.

FIGURE 1.16

The 6 in box 1 must be placed in square (3, 3).

FIGURE 1.17

Examining boxes 1, 2, and 3, we see that boxes 2 and 3 each contain the digit

5, whereas box 1 does not. We deduce that 5 must be placed in square (2, 3)

because rows 1 and 3 already have a 5. In a similar fashion, square (1, 4) must

contain 3. See Figure 1.18.

SOLUTION Recall that each 3 by 3 grid is referred to as a box. For convenience, the boxes are

numbered 1 through 9, starting in the upper left-hand corner and moving from left

to right, and each square can be assigned coordinates (x, y) based on its row num-

ber x and column number y as shown in Figure 1.16.

For example, the digit 2 in Figure 1.16 is in box 1 and has coordinates (1, 3), the

digit 8 is in box 3 and has coordinates (1, 7), the digit 6 is in box 4 and has coordi-

nates (5, 1) and the digit 7 is in box 9 and has coordinates (9, 7).

When you are ﬁrst solving a sudoku puzzle, concentrate on only a few boxes

rather than the puzzle as a whole. For instance, looking at boxes 1, 4, and 7, we see

that boxes 4 and 7 each contain the digit 6, whereas box 1 does not. Consequently,

the 6 in box 1 must be placed in column 3 because (shaded) columns 1 and 2 al-

ready have a 6. However, (shaded) row 2 already has a 6, so we can deduce that 6

must be placed in row 3, column 3, that is, in square (3, 3) as shown in Figure 1.17.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 12

Property

must be placed in row 3, column 3, that is, in square (3, 3) as shown in Figure 1.17.

Property

must be placed in row 3, column 3, that is, in square (3, 3) as shown in Figure 1.17.

that boxes 4 and 7 each contain the digit

in box 1 must be placed in column 3 because (shaded) columns 1 and 2 al-

ready have a

. However, (shaded) row 2 already has a

must be placed in row 3, column 3, that is, in square (3, 3) as shown in Figure 1.17.

Cengage

Box numbers and coordinate system in sudoku.

Cengage

Box numbers and coordinate system in sudoku.

Cengage

For example, the digit 2 in Figure 1.16 is in box 1 and has coordinates (1, 3), the

Cengage

For example, the digit 2 in Figure 1.16 is in box 1 and has coordinates (1, 3), the

digit 8 is in box 3 and has coordinates (1, 7), the digit 6 is in box 4 and has coordi-

Cengage

digit 8 is in box 3 and has coordinates (1, 7), the digit 6 is in box 4 and has coordi-

nates (5, 1) and the digit 7 is in box 9 and has coordinates (9, 7).

Cengage

nates (5, 1) and the digit 7 is in box 9 and has coordinates (9, 7).

When you are ﬁrst solving a sudoku puzzle, concentrate on only a few boxes

Cengage

When you are ﬁrst solving a sudoku puzzle, concentrate on only a few boxes

rather than the puzzle as a whole. For instance, looking at boxes 1, 4, and 7, we see

Cengage

rather than the puzzle as a whole. For instance, looking at boxes 1, 4, and 7, we see

that boxes 4 and 7 each contain the digit

Cengage

that boxes 4 and 7 each contain the digit

in box 1 must be placed in column 3 because (shaded) columns 1 and 2 al-

Cengage

in box 1 must be placed in column 3 because (shaded) columns 1 and 2 al-

. However, (shaded) row 2 already has a

Cengage

. However, (shaded) row 2 already has a

Learning

789

Learning

789

Learning

789

Learning

789

Box numbers and coordinate system in sudoku.

Learning

Box numbers and coordinate system in sudoku.

1.1 Deductive versus Inductive Reasoning 13

Because we have placed two new digits in box 1, we might wish to focus on

the remainder of (shaded) box 1. Notice that the digit 4 can be placed only in

square (3, 1), as row 1 and column 2 already have a 4 in each of them; likewise, the

digit 9 can be placed only in square (1, 1) because column 2 already has a 9.

Finally, either of the digits 1 or 7 can be placed in square (1, 2) or (3, 2) as shown

in Figure 1.19. At some point later in the solution, we will be able to determine the

exact values of squares (1, 2) and (3, 2), that is, which square receives a 1 and

which receives a 7.

Analyzing boxes 1, 2, and 3; placing the digits 3 and 5.

FIGURE 1.18

1,7

Focusing on box 1.

FIGURE 1.19

Using this strategy of analyzing the contents of three consecutive boxes, we

deduce the following placement of digits: 1 must go in (2, 5), 6 must go in (6, 7),

6 must go in (8, 6), 7 must go in (8, 3), 3 must go in (8, 5), 8 must go in (9, 6), and

5 must go in (7, 4). At this point, box 8 is complete as shown in Figure 1.20.

(Remember, each box must contain each of the digits 1 through 9.)

Once again, we use the three consecutive box strategy and deduce the following

placement of digits: 5 must go in (8, 7), 5 must go in (9, 1), 8 must go in (7, 1), 2 must

go in (8, 1), and 1 must go in (7, 3). At this point, box 7 is complete as shown in

Figure 1.21.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 13

Property

1,7

Cengage

square (3, 1), as row 1 and column 2 already have a

Cengage

square (3, 1), as row 1 and column 2 already have a

can be placed only in square (1, 1) because column 2 already has a 9.

Cengage

can be placed only in square (1, 1) because column 2 already has a 9.

Cengage

can be placed in square (1, 2) or (3, 2) as shown

Cengage

can be placed in square (1, 2) or (3, 2) as shown

in Figure 1.19. At some point later in the solution, we will be able to determine the

Cengage

in Figure 1.19. At some point later in the solution, we will be able to determine the

exact values of squares (1, 2) and (3, 2), that is, which square receives a 1 and

Cengage

exact values of squares (1, 2) and (3, 2), that is, which square receives a 1 and

Cengage

1,7

Cengage

1,7

Learning

Because we have placed two new digits in box 1, we might wish to focus on

Learning

Because we have placed two new digits in box 1, we might wish to focus on

the remainder of (shaded) box 1. Notice that the digit

Learning

the remainder of (shaded) box 1. Notice that the digit

square (3, 1), as row 1 and column 2 already have a

Learning

square (3, 1), as row 1 and column 2 already have a

can be placed only in square (1, 1) because column 2 already has a 9.

Learning

can be placed only in square (1, 1) because column 2 already has a 9.

Learning

Analyzing boxes 1, 2, and 3; placing the digits 3 and 5.

Learning

Analyzing boxes 1, 2, and 3; placing the digits 3 and 5.

We now focus on box 4 and deduce the following placement of digits: 1 must

go in (4, 1), 9 must go in (5, 3), 4 must go in (4, 3), 5 must go in (6, 2), 3 must go

in (4, 2), and 2 must go in (5, 2). At this point, box 4 is complete. In addition, we

deduce that 1 must go in (9, 8), and 3 must go in (5, 6) as shown in Figure 1.22.

14 CHAPTER 1 Logic

1,7

Box 8 is complete.

FIGURE 1.20

1,7

Box 7 is complete.

FIGURE 1.21

1,7

Box 4 is complete.

FIGURE 1.22

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 14

Property

We now focus on box 4 and deduce the following placement of digits:

Property

We now focus on box 4 and deduce the following placement of digits:

go in (4, 1),

Property

go in (4, 1),

in (4, 2), and

Property

in (4, 2), and

deduce that

Property

deduce that

Property

Box 7 is complete.

Cengage

Learning

Once again, we use the three consecutive box strategy and deduce the follow-

ing placement of digits: 3 must go in (6, 9), 3 must go in (7, 7), 9 must go in (2, 4),

and 9 must go in (6, 5). Now, to ﬁnish row 6, we place 4 in (6, 8) and 2 in (6, 4) as

shown in Figure 1.23. (Remember, each row must contain each of the digits 1

through 9.)

1.1 Deductive versus Inductive Reasoning 15

After we place 7 in (5, 4), column 4 is complete. (Remember, each column

must contain each of the digits 1 through 9.) This leads to placing 4 in (5, 5) and 8

in (4, 5), thus completing box 5; row 5 is ﬁnalized by placing 8 in (5, 8) as shown

in Figure 1.24.

1,7

Row 6 is complete.

FIGURE 1.23

1,7

Column 4, box 5, and row 5 are complete.

FIGURE 1.24

Now column 7 is completed by placing 4 in (2, 7) and 2 in (3, 7); placing 2 in

(2, 6) and 7 in (3, 6) completes column 6 as shown in Figure 1.25.

At this point, we deduce that the digit in (3, 2) must be 1 because row 3 can-

not have two 7’s. This in turn reveals that 7 must go in (1, 2), and box 1 is now

complete. To complete row 7, we place 4 in (7, 9) and 2 in (7, 8); row 4 is ﬁnished

with 2 in (4, 9) and 7 in (4, 8). See Figure 1.26.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 15

Property

Cengage

After we place

Cengage

After we place

Cengage

in (5, 4), column 4 is complete. (Remember, each column

Cengage

in (5, 4), column 4 is complete. (Remember, each column

must contain each of the digits 1 through 9.) This leads to placing

Cengage

must contain each of the digits 1 through 9.) This leads to placing

in (4, 5), thus completing box 5; row 5 is ﬁnalized by placing

Cengage

in (4, 5), thus completing box 5; row 5 is ﬁnalized by placing

in Figure 1.24.

Cengage

in Figure 1.24.

Cengage

Row 6 is complete.

Cengage

Row 6 is complete.

Learning

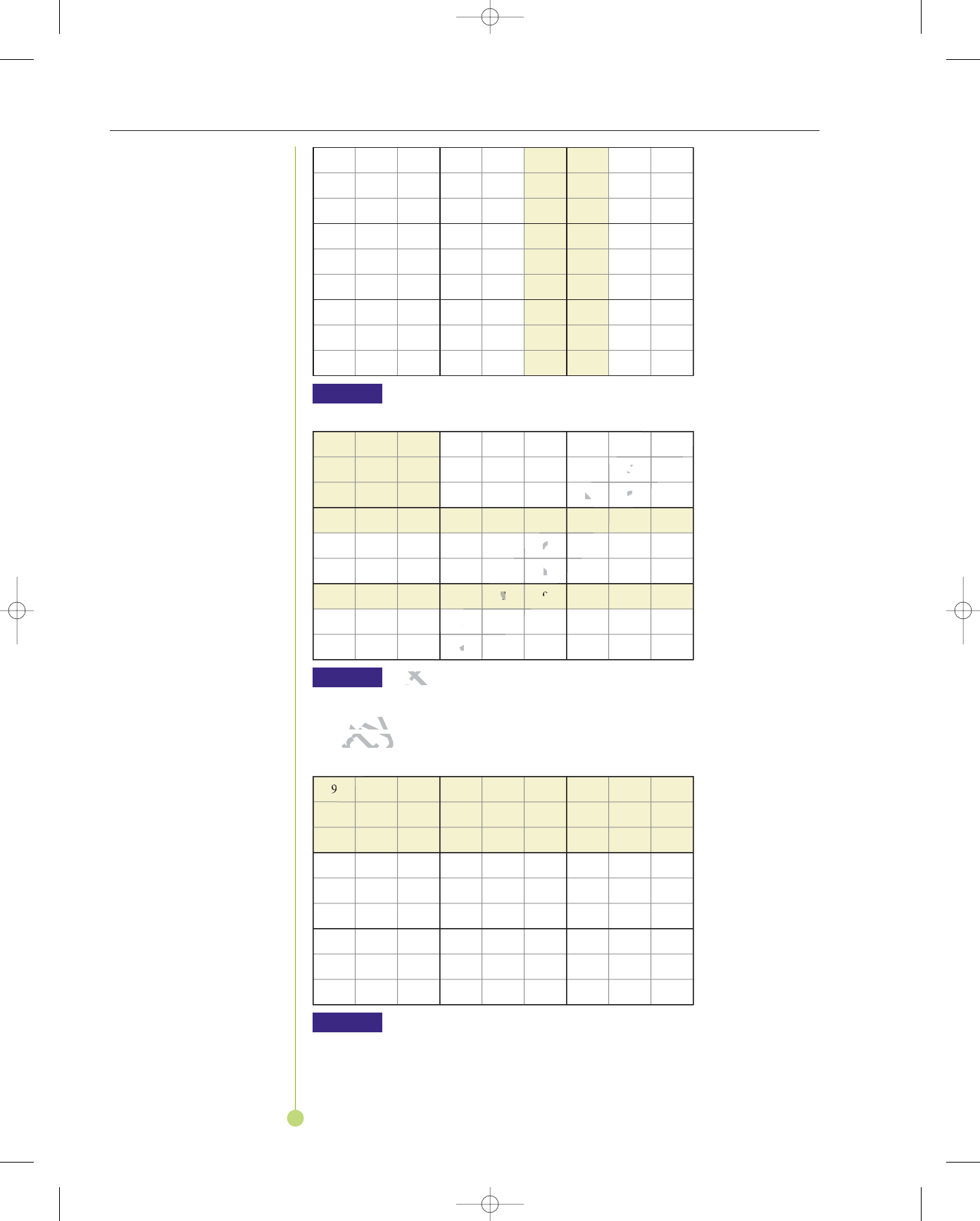
As a ﬁnal check, we scrutinize each box, row, and column to verify that no

box, row, or column contains the same digit twice. Congratulations, the puzzle has

been solved!

To ﬁnish rows 1, 2, and 3, 1 must go in (1, 9), 7 must go in (2, 9), and 9 must

go in (3, 9). The puzzle is now complete as shown in Figure 1.27.

16 CHAPTER 1 Logic

Box 1, row 7, and row 4 are complete.

FIGURE 1.26

1,7

Columns 7 and 6 are complete.

FIGURE 1.25

A completed sudoku puzzle.

FIGURE 1.27

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 16

Property

To ﬁnish rows 1, 2, and 3,

Property

To ﬁnish rows 1, 2, and 3,

go in (3, 9). The puzzle is now complete as shown in Figure 1.27.

Property

go in (3, 9). The puzzle is now complete as shown in Figure 1.27.

Property

Box 1, row 7, and row 4 are complete.

Cengage

Box 1, row 7, and row 4 are complete.

Cengage

Box 1, row 7, and row 4 are complete.

Learning

1.1 Exercises

In Exercises 1–20, construct a Venn diagram to determine the

validity of the given argument.

1. a. 1. All master photographers are artists.

2. Ansel Adams is a master photographer.

Therefore, Ansel Adams is an artist.

b. 1. All master photographers are artists.

2. Ansel Adams is an artist.

Therefore, Ansel Adams is a master photographer.

2. a. 1. All Olympic gold medal winners are role

models.

2. Michael Phelps is an Olympic gold medal

winner.

Therefore, Michael Phelps is a role model.

b. 1. All Olympic gold medal winners are role

models.

2. Michael Phelps is a role model.

Therefore, Michael Phelps is an Olympic gold medal

winner.

3. a. 1. All homeless people are unemployed.

2. Bill Gates is not a homeless person.

Therefore, Bill Gates is not unemployed.

b. 1. All homeless people are unemployed.

2. Bill Gates is not unemployed.

Therefore, Bill Gates is not a homeless person.

4. a. 1. All professional wrestlers are actors.

2. Ralph Nader is not an actor.

Therefore, Ralph Nader is not a professional

wrestler.

b. 1. All professional wrestlers are actors.

2. Ralph Nader is not a professional wrestler.

Therefore, Ralph Nader is not an actor.

5. 1. All pesticides are harmful to the environment.

2. No fertilizer is a pesticide.

Therefore, no fertilizer is harmful to the environment.

6. 1. No one who can afford health insurance is

unemployed.

2. All politicians can afford health insurance.

Therefore, no politician is unemployed.

7. 1. No vegetarian owns a gun.

2. All policemen own guns.

Therefore, no policeman is a vegetarian.

8. 1. No professor is a millionaire.

2. No millionaire is illiterate.

Therefore, no professor is illiterate.

9. 1. All poets are loners.

2. All loners are taxi drivers.

Therefore, all poets are taxi drivers.

10. 1. All forest rangers are environmentalists.

2. All forest rangers are storytellers.

Therefore, all environmentalists are storytellers.

11. 1. Real men don’t eat quiche.

2. Clint Eastwood is a real man.

Therefore, Clint Eastwood doesn’t eat quiche.

12. 1. Real men don’t eat quiche.

2. Oscar Meyer eats quiche.

Therefore, Oscar Meyer isn’t a real man.

13. 1. All roads lead to Rome.

2. Route 66 is a road.

Therefore, Route 66 leads to Rome.

14. 1. All smiling cats talk.

2. The Cheshire Cat smiles.

Therefore, the Cheshire Cat talks.

15. 1. Some animals are dangerous.

2. A tiger is an animal.

Therefore, a tiger is dangerous.

16. 1. Some professors wear glasses.

2. Mr. Einstein wears glasses.

Therefore, Mr. Einstein is a professor.

17. 1. Some women are police ofﬁcers.

2. Some police ofﬁcers ride motorcycles.

Therefore, some women ride motorcycles.

18. 1. All poets are eloquent.

2. Some poets are wine connoisseurs.

Therefore, some wine connoisseurs are eloquent.

19. 1. All squares are rectangles.

2. Some quadrilaterals are squares.

Therefore, some quadrilaterals are rectangles.

20. 1. All squares are rectangles.

2. Some quadrilaterals are rectangles.

Therefore, some quadrilaterals are squares.

21. Classify each argument as deductive or inductive.

a. 1. My television set did not work two nights ago.

2. My television set did not work last night.

Therefore, my television set is broken.

b. 1. All electronic devices give their owners grief.

2. My television set is an electronic device.

Therefore, my television set gives me grief.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 17

Property

2. Ralph Nader is not an actor.

Property

2. Ralph Nader is not an actor.

Therefore, Ralph Nader is not a professional

Property

Therefore, Ralph Nader is not a professional

1. All professional wrestlers are actors.

Property

1. All professional wrestlers are actors.

Property

2. Ralph Nader is not a professional wrestler.

Property

2. Ralph Nader is not a professional wrestler.

Therefore, Ralph Nader is not an actor.

Property

Therefore, Ralph Nader is not an actor.

1. All pesticides are harmful to the environment.

Property

1. All pesticides are harmful to the environment.

Property

2. No fertilizer is a pesticide.

Property

2. No fertilizer is a pesticide.

Therefore, Bill Gates is not a homeless person.

1. All professional wrestlers are actors.

Cengage

Therefore, Bill Gates is not a homeless person.

Cengage

Therefore, Bill Gates is not a homeless person.

1. All smiling cats talk.

Cengage

1. All smiling cats talk.

Cengage

2. The Cheshire Cat smiles.

Cengage

2. The Cheshire Cat smiles.

Therefore, the Cheshire Cat talks.

Cengage

Therefore, the Cheshire Cat talks.

15.

Cengage

15.

Learning

Therefore, Clint Eastwood doesn’t eat quiche.

Learning

Therefore, Clint Eastwood doesn’t eat quiche.

1. Real men don’t eat quiche.

Learning

1. Real men don’t eat quiche.

Learning

2. Oscar Meyer eats quiche.

Learning

2. Oscar Meyer eats quiche.

Therefore, Oscar Meyer isn’t a real man.

Learning

Therefore, Oscar Meyer isn’t a real man.

1. All roads lead to Rome.

Learning

1. All roads lead to Rome.

Learning

2. Route 66 is a road.

Learning

2. Route 66 is a road.

Therefore, Route 66 leads to Rome.

Learning

Therefore, Route 66 leads to Rome.

1. All smiling cats talk.

Learning

1. All smiling cats talk.

18 CHAPTER 1 Logic

22. Classify each argument as deductive or inductive.

a. 1. I ate a chili dog at Joe’s and got indigestion.

2. I ate a chili dog at Ruby’s and got indigestion.

Therefore, chili dogs give me indigestion.

b. 1. All spicy foods give me indigestion.

2. Chili dogs are spicy food.

Therefore, chili dogs give me indigestion.

In Exercises 23–32, ﬁll in the blank with what is most likely to be

the next number. Explain (using complete sentences) the pattern

generated by your answer.

23. 3, 8, 13, 18, _____

24. 10, 11, 13, 16, _____

25. 0, 2, 6, 12, _____

26. 1, 2, 5, 10, _____

27. 1, 4, 9, 16, _____

28. 1, 8, 27, 64, _____

29. 2, 3, 5, 7, 11, _____

30. 1, 1, 2, 3, 5, _____

31. 5, 8, 11, 2, _____

32. 12, 5, 10, 3, _____

In Exercises 33–36, ﬁll in the blanks with what are most likely to

be the next letters. Explain (using complete sentences) the pattern

generated by your answers.

33. O, T, T, F, _____, _____

34. T, F, S, E, _____, _____

35. F, S, S, M, _____, _____

36. J, F, M, A, _____, _____

In Exercises 37–42, explain the general rule or pattern used to

assign the given letter to the given word. Fill in the blank with the

letter that ﬁts the pattern.

37.

38.

39.

40.

41.

42.

43. Find two different numbers that could be used to ﬁll in

the blank.

1, 4, 7, 10, _____

Explain the pattern generated by each of your answers.

44. Find ﬁve different numbers that could be used to ﬁll in

the blank.

7, 14, 21, 28, ______

Explain the pattern generated by each of your

answers.

45. Example 1 utilized the Quadratic Formula. Verify that

is a solution of the equation ax

 bx  c  0.

HINT: Substitute the fraction for x in ax

 bx  c and

simplify.

46. Example 1 utilized the Quadratic Formula. Verify that

is a solution of the equation ax

 bx  c  0.

HINT: Substitute the fraction for x in ax

 bx  c and

simplify.

47. As a review of algebra, use the Quadratic Formula to

solve

 6x  7  0

48. As a review of algebra, use the Quadratic Formula to

solve

 2x  4  0

Solve the sudoku puzzles in Exercises 49–54.

49.

295

2156

x 

b  2b

 4ac

x 

b  2b

 4ac

circle square trapezoid octagon rectangle

c s t o _____

circle square trapezoid octagon rectangle

i u a o _____

circle square trapezoid octagon rectangle

j v b p _____

circle square trapezoid octagon rectangle

c r p g _____

banana strawberry asparagus eggplant orange

bz t u _____

banana strawberry asparagus eggplant orange

yr g p _____

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 18

Property

In Exercises 37–42, explain the general rule or pattern used to

Property

In Exercises 37–42, explain the general rule or pattern used to

assign the given letter to the given word. Fill in the blank with the

Property

assign the given letter to the given word. Fill in the blank with the

Property

circle square trapezoid octagon rectangle

Property

circle square trapezoid octagon rectangle

c s t o _____

Property

c s t o _____

Property

circle square trapezoid octagon rectangle

Property

circle square trapezoid octagon rectangle

Property

c s t o _____

Property

c s t o _____

Property

circle square trapezoid octagon rectangle

Property

circle square trapezoid octagon rectangle

Property

Cengage

is a solution of the equation

Cengage

is a solution of the equation

HINT:

Cengage

HINT:

Substitute the fraction for

Cengage

Substitute the fraction for

simplify.

Cengage

simplify.

Example 1 utilized the Quadratic Formula. Verify that

Cengage

Example 1 utilized the Quadratic Formula. Verify that

Learning

Explain the pattern generated by each of your

Learning

Explain the pattern generated by each of your

Example 1 utilized the Quadratic Formula. Verify that

Learning

Example 1 utilized the Quadratic Formula. Verify that

is a solution of the equation

Learning

is a solution of the equation

Substitute the fraction for

Learning

Substitute the fraction for

Learning

2b2

Learning

2b2

Learning



Learning



Learning

50.

51.

52.

53.

1.1 Exercises 19

54.

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

55. Explain the difference between deductive reasoning

and inductive reasoning.

56. Explain the difference between truth and validity.

57. What is a syllogism? Give an example of a syllogism

that relates to your life.

•

History Questions

58. From the days of the ancient Greeks, the study of

logic has been mandatory in what two professions?

Why?

59. Who developed a formal system of deductive logic

based on arguments?

60. What was the name of the school Aristotle founded?

What does it mean?

61. How did Aristotle’s school of thought differ from

Plato’s?

Web Project

62. Obtain a sudoku puzzle and its solution from a popular

web site. Some useful links for this web project are

listed on the text web site:

www.cengage.com/math/johnson

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 19

Property

Cengage

Explain the difference between deductive reasoning

Cengage

Explain the difference between deductive reasoning

and inductive reasoning.

Cengage

and inductive reasoning.

56.

Cengage

56.

Explain the difference between truth and validity.

Cengage

Explain the difference between truth and validity.

57.

Cengage

57.

What is a syllogism? Give an example of a syllogism

Cengage

What is a syllogism? Give an example of a syllogism

Learning

Answer the following questions using complete

Learning

Answer the following questions using complete

sentences and your own words.

Learning

sentences and your own words.

Concept Questions

Learning

Concept Questions

Explain the difference between deductive reasoning

Learning

Explain the difference between deductive reasoning

and inductive reasoning.

Learning

and inductive reasoning.

Learning

1.2 Symbolic Logic

Objectives

•

Identify simple statements

•

Express a compound statement in symbolic form

•

Create the negation of a statement

•

Express a conditional statement in terms of necessary and sufﬁcient conditions

The syllogism ruled the study of logic for nearly 2,000 years and was not sup-

planted until the development of symbolic logic in the late seventeenth century. As

its name implies, symbolic logic involves the use of symbols and algebraic manip-

ulations in logic.

Statements

All logical reasoning is based on statements. A statement is a sentence that is

either true or false.

EXAMPLE 1 IDENTIFYING STATEMENTS Which of the following are statements? Why

or why not?

a. Apple manufactures computers.

b. Apple manufactures the world’s best computers.

c. Did you buy a Dell?

d. A $2,000 computer that is discounted 25% will cost $1,000.

e. I am telling a lie.

SOLUTION a. The sentence “Apple manufactures computers” is true; therefore, it is a statement.

b. The sentence “Apple manufactures the world’s best computers” is an opinion, and as

such, it is neither true nor false. It is true for some people and false for others. Therefore,

it is not a statement.

c. The sentence “Did you buy a Dell?” is a question. As such, it is neither true nor false; it

is not a statement.

d. The sentence “A $2,000 computer that is discounted 25% will cost $1,000” is false; there-

fore, it is a statement. (A $2,000 computer that is discounted 25% would cost $1,500.)

e. The sentence “I am telling a lie” is a self-contradiction, or paradox. If it were true, the

speaker would be telling a lie, but in telling the truth, the speaker would be contradicting

the statement that he or she was lying; if it were false, the speaker would not be telling a

lie, but in not telling a lie, the speaker would be contradicting the statement that he or she

was lying. The sentence is not a statement.

By tradition, symbolic logic uses lowercase letters as labels for statements.

The most frequently used letters are p, q, r, s, and t. We can label the statement “It

is snowing” as statement p in the following manner:

p: It is snowing.

If it is snowing, p is labeled true, whereas if it is not snowing, p is labeled false.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 20

Property

Did you buy a Dell?

Property

Did you buy a Dell?

A $2,000 computer that is discounted 25% will cost $1,000.

Property

A $2,000 computer that is discounted 25% will cost $1,000.

I am telling a lie.

Property

I am telling a lie.

Property

The sentence “Apple manufactures computers” is true; therefore, it is a statement.

Property

The sentence “Apple manufactures computers” is true; therefore, it is a statement.

Property

The sentence “Apple manufactures the world’s best computers” is an opinion, and as

Property

The sentence “Apple manufactures the world’s best computers” is an opinion, and as

such, it is neither true nor false. It is true for some people and false for others. Therefore,

Property

such, it is neither true nor false. It is true for some people and false for others. Therefore,

Property

Apple manufactures computers.

Apple manufactures the world’s best computers.

Did you buy a Dell?

Cengage

All logical reasoning is based on statements. A

Cengage

All logical reasoning is based on statements. A

IDENTIFYING STATEMENTS

Cengage

IDENTIFYING STATEMENTS

Apple manufactures computers.

Cengage

Apple manufactures computers.

Learning

Express a conditional statement in terms of necessary and sufﬁcient conditions

Learning

Express a conditional statement in terms of necessary and sufﬁcient conditions

The syllogism ruled the study of logic for nearly 2,000 years and was not sup-

Learning

The syllogism ruled the study of logic for nearly 2,000 years and was not sup-

planted until the development of symbolic logic in the late seventeenth century. As

Learning

planted until the development of symbolic logic in the late seventeenth century. As

its name implies, symbolic logic involves the use of symbols and algebraic manip-

Learning

its name implies, symbolic logic involves the use of symbols and algebraic manip-

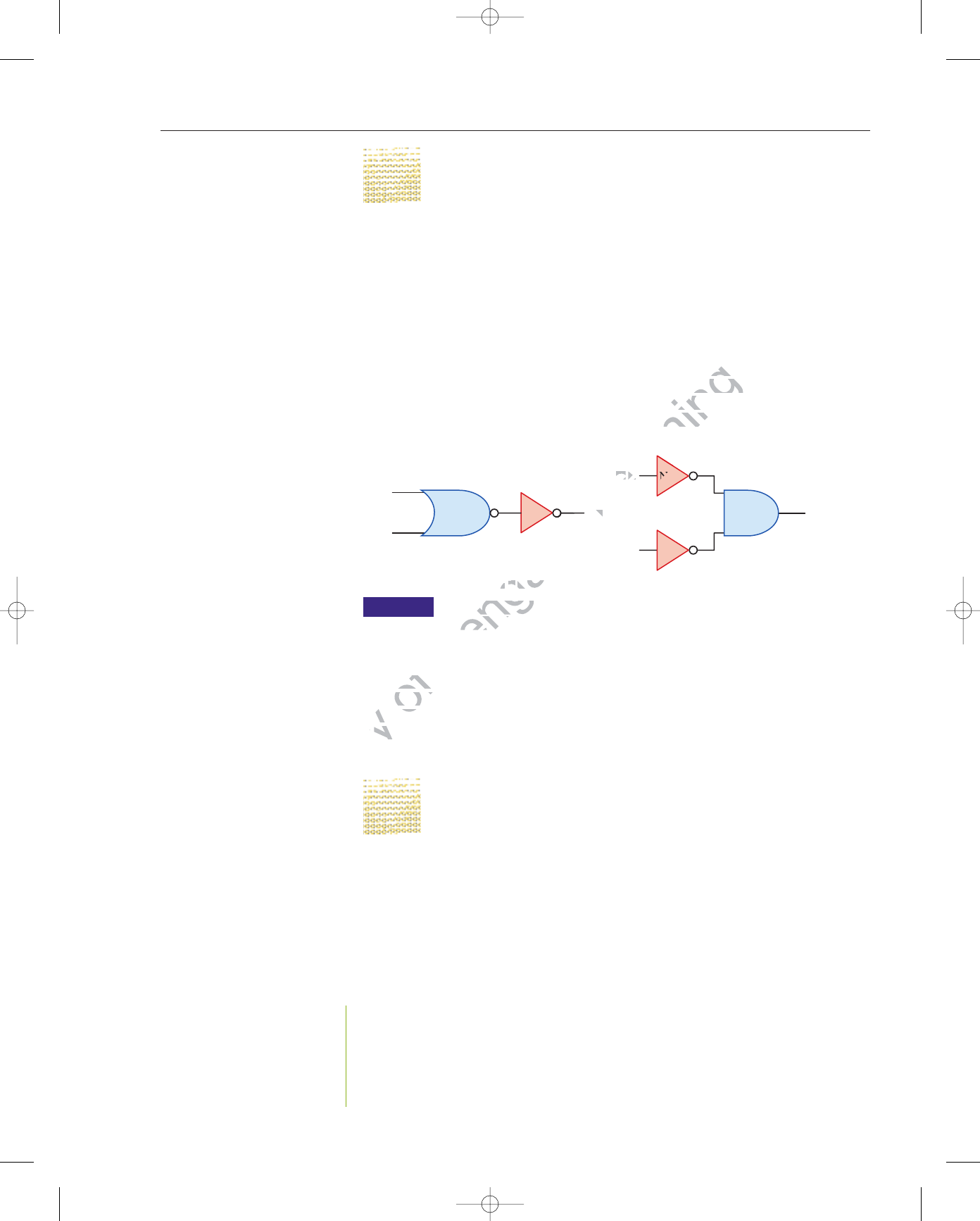
Compound Statements and Logical Connectives

It is easy to determine whether a statement such as “Charles donated blood” is true

or false; either he did or he didn’t. However, not all statements are so simple; some

are more involved. For example, the truth of “Charles donated blood and did not

wash his car, or he went to the library,” depends on the truth of the individual

pieces that make up the larger, compound statement. A compound statement is a

statement that contains one or more simpler statements. Acompound statement can

be formed by inserting the word not into a simpler statement or by joining two or

more statements with connective words such as and, or, if ... then ... , only if, and

if and only if. The compound statement “Charles did not wash his car” is formed

from the simpler statement “Charles did wash his car.” The compound statement

“Charles donated blood and did not wash his car, or he went to the library” consists

of three statements, each of which may be true or false.

Figure 1.28 diagrams two equivalent compound statements.

1.2 Symbolic Logic 21

out

in A

in B

in A

in B

Or Not

out

“neither A nor B” “not A and not B”means

Not

And

Technicians and engineers use compound statements and logical

connectives to study the ﬂow of electricity through switching circuits.

FIGURE 1.28

When is a compound statement true? Before we can answer this question, we

must ﬁrst examine the various ways in which statements can be connected. Depend-

ing on how the statements are connected, the resulting compound statement can be

a negation, a conjunction, a disjunction, a conditional, or any combination thereof.

The Negation p

The negation of a statement is the denial of the statement and is represented by the

symbol . The negation is frequently formed by inserting the word not. For exam-

ple, given the statement “p: It is snowing,” the negation would be “p: It is not

snowing.” If it is snowing, p is true and p is false. Similarly, if it is not snowing,

p is false and p is true. A statement and its negation always have opposite truth

values; when one is true, the other is false. Because the truth of the negation de-

pends on the truth of the original statement, a negation is classiﬁed as a compound

statement.

EXAMPLE 2 WRITING A NEGATION Write a sentence that represents the negation of each

statement:

a. The senator is a Democrat. b. The senator is not a Democrat.

c. Some senators are Republicans. d. All senators are Republicans.

e. No senator is a Republican.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 21

Property

must ﬁrst examine the various ways in which statements can be connected. Depend-

Property

must ﬁrst examine the various ways in which statements can be connected. Depend-

ing on how the statements are connected, the resulting compound statement can be

Property

ing on how the statements are connected, the resulting compound statement can be

Property

negation,

Property

negation,

When is a compound statement true? Before we can answer this question, we

must ﬁrst examine the various ways in which statements can be connected. Depend-

ing on how the statements are connected, the resulting compound statement can be

Cengage

nor

Cengage

nor

Cengage

” “not

Cengage

” “not

Cengage

Technicians and engineers use compound statements and logical

Cengage

Technicians and engineers use compound statements and logical

connectives to study the ﬂow of electricity through switching circuits.

Cengage

connectives to study the ﬂow of electricity through switching circuits.

When is a compound statement true? Before we can answer this question, we

Cengage

When is a compound statement true? Before we can answer this question, we

Learning

pler statement “Charles did wash his car.” The compound statement

Learning

pler statement “Charles did wash his car.” The compound statement

he went to the library” consists

Learning

he went to the library” consists

of three statements, each of which may be true or false.

Learning

of three statements, each of which may be true or false.

Figure 1.28 diagrams two equivalent compound statements.

Learning

Figure 1.28 diagrams two equivalent compound statements.

Learning

out

Learning

out

Not

Learning

Not

SOLUTION a. The negation of “The senator is a Democrat” is “The senator is not a Democrat.”

b. The negation of “The senator is not a Democrat” is “The senator is a Democrat.”

c. A common error would be to say that the negation of “Some senators are Republicans”

is “Some senators are not Republicans.” However, “Some senators are Republicans” is

not denied by “Some senators are not Republicans.” The statement “Some senators are

Republicans” implies that at least one senator is a Republican. The negation of this state-

ment is “It is not the case that at least one senator is a Republican,” or (more commonly

phrased) the negation is “No senator is a Republican.”

d. The negation of “All senators are Republicans” is “It is not the case that all senators are

Republicans,” or “There exists a senator who is not a Republican,” or (more commonly

phrased) “Some senators are not Republicans.”

e. The negation of “No senator is a Republican” is “It is not the case that no senator is a

Republican” or, in other words, “There exists at least one senator who is a Republican.”

If “some” is interpreted as meaning “at least one,” the negation can be expressed as

“Some senators are Republicans.”

The words some, all, and no (or none) are referred to as quantiﬁers. Parts (c)

through (e) of Example 2 contain quantiﬁers. The linked pairs of quantiﬁed state-

ments shown in Figure 1.29 are negations of each other.

22 CHAPTER 1 Logic

All p are q.

Some p are q.

No p are q.

Some p are not q.

Negations of statements containing quantiﬁers.FIGURE 1.29

The Conjunction p ∧ q

Consider the statement “Norma Rae is a union member and she is a Democrat.”

This is a compound statement, because it consists of two statements—“Norma Rae

is a union member” and “she (Norma Rae) is a Democrat”—and the connective

word and. Such a compound statement is referred to as a conjunction. A conjunc-

tion consists of two or more statements connected by the word and. We use the

symbol ∧ to represent the word and; thus, the conjunction “p ∧ q” represents the

compound statement “p and q.”

EXAMPLE 3 TRANSLATING WORDS INTO SYMBOLS Using the symbolic represen-

tations

p: Norma Rae is a union member.

q: Norma Rae is a Democrat.

express the following compound statements in symbolic form:

a. Norma Rae is a union member and she is a Democrat.

b. Norma Rae is a union member and she is not a Democrat.

SOLUTION a. The compound statement “Norma Rae is a union member and she is a Democrat” can be

represented as p ∧ q.

b. The compound statement “Norma Rae is a union member and she is not a Democrat”

can be represented as p ∧ q.

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 22

Property

Consider the statement “Norma Rae is a union member and she is a Democrat.”

Property

Consider the statement “Norma Rae is a union member and she is a Democrat.”

This is a compound statement, because it consists of two statements—“Norma Rae

Property

This is a compound statement, because it consists of two statements—“Norma Rae

is a union member” and “she (Norma Rae) is a Democrat”—and the connective

Property

is a union member” and “she (Norma Rae) is a Democrat”—and the connective

word

Property

word

and.

Property

and.

tion

Property

tion

consists of two or more statements connected by the word

Property

consists of two or more statements connected by the word

symbol

Property

symbol

compound statement “

Property

compound statement “

Property

The Conjunction

Consider the statement “Norma Rae is a union member and she is a Democrat.”

Cengage

Some

Cengage

Some

Cengage

are not

Cengage

are not

Cengage

Negations of statements containing quantiﬁers.

Cengage

Negations of statements containing quantiﬁers.

The Conjunction

Cengage

The Conjunction

Learning

Republican” or, in other words, “There exists at least one senator who

Learning

Republican” or, in other words, “There exists at least one senator who

Learning

If “some” is interpreted as meaning “at least one,” the negation can be expressed as

Learning

If “some” is interpreted as meaning “at least one,” the negation can be expressed as

) are referred to as

Learning

) are referred to as

quantiﬁers.

Learning

quantiﬁers.

through (e) of Example 2 contain quantiﬁers. The linked pairs of quantiﬁed state-

Learning

through (e) of Example 2 contain quantiﬁers. The linked pairs of quantiﬁed state-

ments shown in Figure 1.29 are negations of each other.

Learning

ments shown in Figure 1.29 are negations of each other.

Learning

The Disjunction p ∨ q

When statements are connected by the word or, a disjunction is formed. We use

the symbol ∨ to represent the word or. Thus, the disjunction “p ∨ q” represents the

compound statement “p or q.” We can interpret the word or in two ways. Consider

the statements

p: Kaitlin is a registered Republican.

q: Paki is a registered Republican.

The statement “Kaitlin is a registered Republican or Paki is a registered Republi-

can” can be symbolized as p ∨ q. Notice that it is possible that both Kaitlin and

Paki are registered Republicans. In this example, or includes the possibility that

both things may happen. In this case, we are working with the inclusive or.

Now consider the statements

p: Kaitlin is a registered Republican.

q: Kaitlin is a registered Democrat.

The statement “Kaitlin is a registered Republican or Kaitlin is a registered Demo-

crat” does not include the possibility that both may happen; one statement excludes

the other. When this happens, we are working with the exclusive or. In our study

of symbolic logic (as in most mathematics), we will always use the inclusive or.

Therefore, “p or q” means “p or q or both.”

EXAMPLE 4 TRANSLATING SYMBOLS INTO WORDS Using the symbolic represen-

tations

p: Juanita is a college graduate.

q: Juanita is employed.

express the following compound statements in words:

a. p ∨ q b. p ∧ q

c. p ∨ q d. p ∧ q

SOLUTION a. p ∨ q represents the statement “Juanita is a college graduate or Juanita is employed (or

both).”

b. p ∧ q represents the statement “Juanita is a college graduate and Juanita is employed.”

c. p ∨ q represents the statement “Juanita is a college graduate or Juanita is not

employed.”

d. p ∧ q represents the statement “Juanita is not a college graduate and Juanita is

employed.”

The Conditional p → q

Consider the statement “If it is raining, then the streets are wet.” This is a com-

pound statement because it connects two statements, namely, “it is raining” and

“the streets are wet.” Notice that the statements are connected with “if . . . then . . .”

phrasing. Any statement of the form “if p then q” is called a conditional (or an

implication); p is called the hypothesis (or premise) of the conditional, and q is

called the conclusion of the conditional. The conditional “if p then q” is repre-

sented by the symbols “p → q” (p implies q). When people use conditionals in

1.2 Symbolic Logic 23

95057_01_ch01_p001-066.qxd 9/27/10 9:33 AM Page 23

Property

∨

Property

∨

SOLUTION

Property

SOLUTION

Property

Juanita is employed.

express the following compound statements in words:

∨

Cengage

include the possibility that both may happen; one statement

Cengage

include the possibility that both may happen; one statement

the other. When this happens, we are working with the

Cengage

the other. When this happens, we are working with the

of symbolic logic (as in most mathematics), we will always use the

Cengage

of symbolic logic (as in most mathematics), we will always use the

” means “

Cengage

” means “

Cengage

” means “p” means “

Cengage

” means “p” means “

Cengage

or both.”

Cengage

or both.”

TRANSLATING SYMBOLS INTO WORDS

Cengage

TRANSLATING SYMBOLS INTO WORDS

Juanita is a college graduate.

Cengage

Juanita is a college graduate.

Juanita is employed.

Cengage

Juanita is employed.

express the following compound statements in words:

Cengage

express the following compound statements in words:

Learning

Notice that it is possible that

Learning

Notice that it is possible that

includes the possibility that

Learning

includes the possibility that

both things may happen. In this case, we are working with the

Learning

both things may happen. In this case, we are working with the

Kaitlin is a registered Democrat.

Learning

Kaitlin is a registered Democrat.

The statement “Kaitlin is a registered Republican or Kaitlin is a registered Demo-

Learning

The statement “Kaitlin is a registered Republican or Kaitlin is a registered Demo-

include the possibility that both may happen; one statement

Learning

include the possibility that both may happen; one statement

the other. When this happens, we are working with the

Learning

the other. When this happens, we are working with the

24 CHAPTER 1 Logic

GOTTFRIED WILHELM LEIBNIZ 1646–1716

Leibniz’s afﬁnity

for logic was char-

acterized by his

search for a charac-

teristica universalis,

or “universal charac-

ter.” Leibniz be-

lieved that by com-

bining logic and

mathematics, a gen-

eral symbolic lan-

guage could be created in which all

scientiﬁc problems could be solved with

a minimum of effort. In this universal

language, statements and the logical

relationships between them would be

represented by letters and symbols. In

In the early 1670s, Leibniz invented one of the world’s ﬁrst mechanical

calculating machines. Leibniz’s machine could multiply and divide, whereas

an earlier machine invented by Blaise Pascal (see Chapter 3) could only add

and subtract.

Leibniz’s words, “All truths of reason

would be reduced to a kind of calculus,

and the errors would only be errors of

computation.” In essence, Leibniz be-

lieved that once a problem had been

translated into this universal language of

symbolic logic, it would be solved auto-

matically by simply applying the mathe-

matical rules that governed the manipu-

lation of the symbols.

Leibniz’s work in the ﬁeld of symbolic

logic did not arouse much academic cu-

riosity; many say that it was too far

ahead of its time. The study of symbolic

logic was not systematically investigated

again until the nineteenth century.

n addition to cofounding

calculus (see Chapter 13),

the German-born Gottfried

Wilhelm Leibniz contributed

much to the development of

symbolic logic. A precocious

child, Leibniz was self-taught in

many areas. He taught himself

Latin at the age of eight and began

the study of Greek when he was twelve.

In the process, he was exposed to the

writings of Aristotle and became in-

trigued by formalized logic.

At the age of ﬁfteen, Leibniz entered

the University of Leipzig to study law. He

received his bachelor’s degree two

years later, earned his master’s degree

the following year, and then transferred

to the University of Nuremberg.

Leibniz received his doctorate in law

within a year and was immediately

offered a professorship but refused it,

saying that he had “other things in

mind.” Besides law, these “other things”

included politics, religion, history, litera-

ture, metaphysics, philosophy, logic,

and mathematics. Thereafter, Leibniz

worked under the sponsorship of the

courts of various nobles, serving as

lawyer, historian, and librarian to the

elite. At one point, Leibniz was offered

the position of librarian at the Vatican

but declined the offer.

Historical

Note

everyday speech, they often omit the word then, as in “If it is raining, the streets

are wet.” Alternatively, the conditional “if p then q” may be phrased as “q if p”

(“The streets are wet if it is raining”).

EXAMPLE 5 TRANSLATING WORDS INTO SYMBOLS Using the symbolic represen-

tations

p: I am healthy.

q: I eat junk food.

r: I exercise regularly.

express the following compound statements in symbolic form:

a. I am healthy if I exercise regularly.

b. If I eat junk food and do not exercise, then I am not healthy.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 24

Property

lawyer, historian, and librarian to the

Property

lawyer, historian, and librarian to the

elite. At one point, Leibniz was offered

Property

elite. At one point, Leibniz was offered

the position of librarian at the Vatican

Property

the position of librarian at the Vatican

Cengage

Learning

matically by simply applying the mathe-

Learning

matically by simply applying the mathe-

matical rules that governed the manipu-

Learning

matical rules that governed the manipu-

lation of the symbols.

Learning

lation of the symbols.

Leibniz’s work in the ﬁeld of symbolic

Learning

Leibniz’s work in the ﬁeld of symbolic

logic did not arouse much academic cu-

Learning

logic did not arouse much academic cu-

riosity; many say that it was too far

Learning

riosity; many say that it was too far

ahead of its time. The study of symbolic

Learning

ahead of its time. The study of symbolic

logic was not systematically investigated

Learning

logic was not systematically investigated

again until the nineteenth century.

Learning

again until the nineteenth century.

1.2 Symbolic Logic 25

SOLUTION a. “I am healthy if I exercise regularly” is a conditional (if ... then . . . ) and can be re-

phrased as follows:

“ I exercise regularly, I am healthy.”

Statement r Statement p

is the premise. is the conclusion.

The given compound statement can be expressed as r → p.

b. “If I eat junk food and do not exercise, then I am not healthy” is a conditional

(if ... then . . . ) that contains a conjunction (and) and two negations (not):

“If I eat junk food do exercise, then I am healthy.”

The premise contains The conclusion

a conjunction and a negation. contains a negation.

The premise of the conditional can be represented by q ∧ r, while the conclusion

can be represented by p. Thus, the given compound statement has the symbolic form

(q ∧ r) → p.

EXAMPLE 6 TRANSLATING WORDS INTO SYMBOLS Express the following statements

in symbolic form:

a. All mammals are warm-blooded.

b. No snake is warm-blooded.

SOLUTION a. The statement “All mammals are warm-blooded” can be rephrased as “If it is a mam-

mal, then it is warm-blooded.” Therefore, we deﬁne two simple statements p and q as

p: It is a mammal.

q: It is warm-blooded.

The statement now has the form

“ it is a mammal, it is warm-blooded.”

Statement p Statement q

is the premise. is the conclusion.

and can be expressed as p → q. In general, any statement of the form “All p are q” can

be symbolized as p → q.

b. The statement “No snake is warm-blooded” can be rephrased as “If it is a snake, then it

is not warm-blooded.” Therefore, we deﬁne two simple statements p and q as

p: It is a snake.

q: It is warm-blooded.

The statement now has the form

“ it is a snake, it is warm-blooded.”

Statement p The negation of statement q

is the premise. is the conclusion.

and can be expressed as p → q. In general, any statement of the form “No p is q” can

be symbolized as p → q.

↑↑↑↑

notthenIf

↑↑↑↑

thenIf

↑↑↑↑

notnotand

↑↑↑↑

thenIf

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 25

Property

It is warm-blooded.

The statement now has the form

Cengage

TRANSLATING WORDS INTO SYMBOLS

Cengage

TRANSLATING WORDS INTO SYMBOLS

All mammals are warm-blooded.

Cengage

All mammals are warm-blooded.

No snake is warm-blooded.

Cengage

No snake is warm-blooded.

The statement “All mammals are warm-blooded” can be rephrased as “If it is a mam-

Cengage

The statement “All mammals are warm-blooded” can be rephrased as “If it is a mam-

mal, then it is warm-blooded.” Therefore, we deﬁne two simple statements

Cengage

mal, then it is warm-blooded.” Therefore, we deﬁne two simple statements

It is a mammal.

Cengage

It is a mammal.

It is warm-blooded.

Cengage

It is warm-blooded.

Learning

The premise contains The conclusion

Learning

The premise contains The conclusion

a conjunction and a negation. contains a negation.

Learning

a conjunction and a negation. contains a negation.

The premise of the conditional can be represented by

Learning

The premise of the conditional can be represented by

Learning

∧

Learning

∧



Learning



Thus, the given compound statement has the symbolic form

Learning

Thus, the given compound statement has the symbolic form

TRANSLATING WORDS INTO SYMBOLS

Learning

TRANSLATING WORDS INTO SYMBOLS

Learning

↑↑

Learning

↑↑

26 CHAPTER 1 Logic

Necessary and Sufﬁcient Conditions

As Example 6 shows, conditionals are not always expressed in the form “if p then

q.” In addition to “all p are q,” other standard forms of a conditional include state-

ments that contain the word sufﬁcient or necessary.

Consider the statement “Being a mammal is sufﬁcient for being warm-

blooded.” One deﬁnition of the word sufﬁcient is “adequate.” Therefore, “being a

mammal” is an adequate condition for “being warm-blooded”; hence, “being a mam-

mal” implies “being warm-blooded.” Logically, the statement “Being a mammal is

sufﬁcient for being warm-blooded” is equivalent to saying “If it is a mammal, then it

is warm-blooded.” Consequently, the general statement “p is sufﬁcient for q” is an

alternative form of the conditional “if p then q” and can be symbolized as p

→ q.

“Being a mammal” is a sufﬁcient (adequate) condition for “being warm-

blooded,” but is it a necessary condition? Of course not: some animals are warm-

blooded but are not mammals (chickens, for example). One deﬁnition of the word

necessary is “required.” Therefore, “being a mammal” is not required for “being

warm-blooded.” However, is “being warm-blooded” a necessary (required) condi-

tion for “being a mammal”? Of course it is: all mammals are warm-blooded (that is,

there are no cold-blooded mammals). Logically, the statement “being warm-blooded

is necessary for being a mammal” is equivalent to saying “If it is a mammal, then it

is warm-blooded.” Consequently, the general statement “q is necessary for p” is an

alternative form of the conditional “if p then q” and can be symbolized as p

→ q.

In summary, a sufﬁcient condition is the hypothesis or premise of a condi-

tional statement, whereas a necessary condition is the conclusion of a conditional

statement.

p: hypothesis p implies qq: conclusion

EXAMPLE 7 TRANSLATING WORDS INTO SYMBOLS Using the symbolic represen-

tations

p: A person obeys the law.

q: A person is arrested.

express the following compound statements in symbolic form:

a. Being arrested is necessary for not obeying the law.

b. Obeying the law is sufﬁcient for not being arrested.

SOLUTION a. “Being arrested” is a necessary condition; hence, “a person is arrested” is the conclusion

of a conditional statement.

A necessary condition.

Therefore, the statement “Being arrested is necessary for not obeying the law” can be

rephrased as follows:

“ a person does obey the law, the person is arrested.”

The negation of statement p Statement q is the

is the premise. conclusion.

The given compound statement can be expressed as p → q.

↑↑

thennotIf

A person is

arrested.

A person does

not obey the law.

Necessary conditionSufﬁcient condition

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 26

Property

TRANSLATING WORDS INTO SYMBOLS

Property

TRANSLATING WORDS INTO SYMBOLS

tations

Property

tations

Property

A person obeys the law.

Property

A person obeys the law.

Property

A person is arrested.

Property

A person is arrested.

express the following compound statements in symbolic form:

Property

express the following compound statements in symbolic form:

Property

Being arrested is necessary for not obeying the law.

Property

Being arrested is necessary for not obeying the law.

Property

TRANSLATING WORDS INTO SYMBOLS

Cengage

is necessary for being a mammal” is equivalent to saying “If it is a mammal, then it

Cengage

is necessary for being a mammal” is equivalent to saying “If it is a mammal, then it

is warm-blooded.” Consequently, the general statement “

Cengage

is warm-blooded.” Consequently, the general statement “

alternative form of the conditional “if

Cengage

alternative form of the conditional “if

Cengage

then

Cengage

then

Cengage

” and can be symbolized as

Cengage

” and can be symbolized as

In summary, a sufﬁcient condition is the hypothesis or premise of a condi-

Cengage

In summary, a sufﬁcient condition is the hypothesis or premise of a condi-

tional statement, whereas a necessary condition is the conclusion of a conditional

Cengage

tional statement, whereas a necessary condition is the conclusion of a conditional

hypothesis

Cengage

hypothesis

Sufﬁcient condition

Cengage

Sufﬁcient condition

Cengage

Learning

” and can be symbolized as

Learning

” and can be symbolized as

(adequate) condition for “being warm-

Learning

(adequate) condition for “being warm-

condition? Of course not: some animals are warm-

Learning

condition? Of course not: some animals are warm-

blooded but are not mammals (chickens, for example). One deﬁnition of the word

Learning

blooded but are not mammals (chickens, for example). One deﬁnition of the word

is “required.” Therefore, “being a mammal” is not required for “being

Learning

is “required.” Therefore, “being a mammal” is not required for “being

warm-blooded.” However, is “being warm-blooded” a necessary (required) condi-

Learning

warm-blooded.” However, is “being warm-blooded” a necessary (required) condi-

tion for “being a mammal”? Of course it is: all mammals

Learning

tion for “being a mammal”? Of course it is: all mammals

are

Learning

are

there are no cold-blooded mammals). Logically, the statement “being warm-blooded

Learning

there are no cold-blooded mammals). Logically, the statement “being warm-blooded

is necessary for being a mammal” is equivalent to saying “If it is a mammal, then it

Learning

is necessary for being a mammal” is equivalent to saying “If it is a mammal, then it

is warm-blooded.” Consequently, the general statement “

Learning

is warm-blooded.” Consequently, the general statement “

b. “Obeying the law” is a sufﬁcient condition; hence, “A person obeys the law” is the

premise of a conditional statement.

A sufﬁcient condition.

Therefore, the statement “Obeying the law is sufﬁcient for not being arrested” can be

rephrased as follows:

“ a person obeys the law, the person is arrested.”

Statement p The negation of statement q

is the premise. is the conclusion.

The given compound statement can be expressed as p → q.

↑↑

notthenIf

A person is not arrested.A person obeys the law.

1.2 Exercises 27

Statement Symbol Read as . . .

negation p not p

conjunction p ∧ qpand q

disjunction p ∨ qpor q

conditional p

→ q if p, then q

(implication) p is sufﬁcient for q

q is necessary for p

Logical connectives.FIGURE 1.30

We have seen that a statement is a sentence that is either true or false and that

connecting two or more statements forms a compound statement. Figure 1.30 sum-

marizes the logical connectives and symbols that were introduced in this section.

The various connectives have been deﬁned; we can now proceed in our analysis of

the conditions under which a compound statement is true. This analysis is carried

out in the next section.

1.2 Exercises

1. Which of the following are statements? Why or why

not?

a. George Washington was the ﬁrst president of the

United States.

b. Abraham Lincoln was the second president of the

United States.

c. Who was the ﬁrst vice president of the United

States?

d. Abraham Lincoln was the best president.

2. Which of the following are statements? Why or why

not?

a. 3  5  6

b. Solve the equation 2x  5  3.

c. x

 1  0 has no solution.

d. x

 1  (x  1)(x  1)

e. Is a rational number?12

3. Determine which pairs of statements are negations of

each other.

a. All of the fruits are red.

b. None of the fruits is red.

c. Some of the fruits are red.

d. Some of the fruits are not red.

4. Determine which pairs of statements are negations of

each other.

a. Some of the beverages contain caffeine.

b. Some of the beverages do not contain caffeine.

c. None of the beverages contain caffeine.

d. All of the beverages contain caffeine.

5. Write a sentence that represents the negation of each

statement.

a. Her dress is not red.

b. Some computers are priced under $100.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 27

Property

xercises

Property

xercises

Which of the following are statements? Why or why

Property

Which of the following are statements? Why or why

George Washington was the ﬁrst president of the

Property

George Washington was the ﬁrst president of the

United States.

Property

United States.

FIGURE 1.30

Cengage

Statement Symbol Read as . . .

Cengage

Statement Symbol Read as . . .

Cengage

not

Cengage

not

Cengage

and

Cengage

and

Cengage

∨

Cengage

∨

Cengage

→

Cengage

→

Cengage

(implication)

Cengage

(implication)

Cengage

Learning



Learning



Learning

We have seen that a statement is a sentence that is either true or false and that

Learning

We have seen that a statement is a sentence that is either true or false and that

connecting two or more statements forms a compound statement. Figure 1.30 sum-

Learning

connecting two or more statements forms a compound statement. Figure 1.30 sum-

marizes the logical connectives and symbols that were introduced in this section.

Learning

marizes the logical connectives and symbols that were introduced in this section.

The various connectives have been deﬁned; we can now proceed in our analysis of

Learning

The various connectives have been deﬁned; we can now proceed in our analysis of

the conditions under which a compound statement is true. This analysis is carried

Learning

the conditions under which a compound statement is true. This analysis is carried

f. Riding a motorcycle or playing the guitar is neces-

sary for wearing a leather jacket.

10. Using the symbolic representations

p: The car costs $70,000.

q: The car goes 140 mph.

r: The car is red.

express the following compound statements in sym-

bolic form.

a. All red cars go 140 mph.

b. The car is red, goes 140 mph, and does not cost

$70,000.

c. If the car does not cost $70,000, it does not go

140 mph.

d. The car is red and it does not go 140 mph or cost

$70,000.

e. Being able to go 140 mph is sufﬁcient for a car to

cost $70,000 or be red.

f. Not being red is necessary for a car to cost $70,000

and not go 140 mph.

In Exercises 11–34, translate the sentence into symbolic form. Be

sure to deﬁne each letter you use. (More than one answer is

possible.)

11. All squares are rectangles.

12. All people born in the United States are American

citizens.

13. No square is a triangle.

14. No convicted felon is eligible to vote.

15. All whole numbers are even or odd.

16. All muscle cars from the Sixties are polluters.

17. No whole number is greater than 3 and less than 4.

18. No electric-powered car is a polluter.

19. Being an orthodontist is sufﬁcient for being a dentist.

20. Being an author is sufﬁcient for being literate.

21. Knowing Morse code is necessary for operating a

telegraph.

22. Knowing CPR is necessary for being a paramedic.

23. Being a monkey is sufﬁcient for not being an ape.

24. Being a chimpanzee is sufﬁcient for not being a

monkey.

25. Not being a monkey is necessary for being an ape.

26. Not being a chimpanzee is necessary for being a

monkey.

27. I do not sleep soundly if I drink coffee or eat

chocolate.

28. I sleep soundly if I do not drink coffee or eat

chocolate.

29. Your check is not accepted if you do not have a driver’s

license or a credit card.

30. Your check is accepted if you have a driver’s license or

a credit card.

31. If you drink and drive, you are ﬁned or you go to jail.

c. All dogs are four-legged animals.

d. No sleeping bag is waterproof.

6. Write a sentence that represents the negation of each

statement.

a. She is not a vegetarian.

b. Some elephants are pink.

c. All candy promotes tooth decay.

d. No lunch is free.

7. Using the symbolic representations

p: The lyrics are controversial.

q: The performance is banned.

express the following compound statements in sym-

bolic form.

a. The lyrics are controversial, and the performance is

banned.

b. If the lyrics are not controversial, the performance

is not banned.

c. It is not the case that the lyrics are controversial or

the performance is banned.

d. The lyrics are controversial, and the performance is

not banned.

e. Having controversial lyrics is sufﬁcient for banning

a performance.

f. Noncontroversial lyrics are necessary for not ban-

ning a performance.

8. Using the symbolic representations

p: The food is spicy.

q: The food is aromatic.

express the following compound statements in sym-

bolic form.

a. The food is aromatic and spicy.

b. If the food isn’t spicy, it isn’t aromatic.

c. The food is spicy, and it isn’t aromatic.

d. The food isn’t spicy or aromatic.

e. Being nonaromatic is sufﬁcient for food to be

nonspicy.

f. Being spicy is necessary for food to be aromatic.

9. Using the symbolic representations

p: A person plays the guitar.

q: A person rides a motorcycle.

r: A person wears a leather jacket.

express the following compound statements in sym-

bolic form.

a. If a person plays the guitar or rides a motorcycle,

then the person wears a leather jacket.

b. A person plays the guitar, rides a motorcycle, and

wears a leather jacket.

c. A person wears a leather jacket and doesn’t play the

guitar or ride a motorcycle.

d. All motorcycle riders wear leather jackets.

e. Not wearing a leather jacket is sufﬁcient for not

playing the guitar or riding a motorcycle.

28 CHAPTER 1 Logic

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 28

Property

If the food isn’t spicy, it isn’t aromatic.

Property

If the food isn’t spicy, it isn’t aromatic.

The food is spicy, and it isn’t aromatic.

Property

The food is spicy, and it isn’t aromatic.

The food isn’t spicy or aromatic.

Property

The food isn’t spicy or aromatic.

Being nonaromatic is sufﬁcient for food to be

Property

Being nonaromatic is sufﬁcient for food to be

Being spicy is necessary for food to be aromatic.

Property

Being spicy is necessary for food to be aromatic.

Using the symbolic representations

Property

Using the symbolic representations

A person plays the guitar.

Property

A person plays the guitar.

express the following compound statements in sym-

Cengage

In Exercises 11–34, translate the sentence into symbolic form. Be

Cengage

In Exercises 11–34, translate the sentence into symbolic form. Be

sure to deﬁne each letter you use. (More than one answer is

Cengage

sure to deﬁne each letter you use. (More than one answer is

possible.)

Cengage

possible.)

11.

Cengage

11.

All squares are rectangles.

Cengage

All squares are rectangles.

12.

Cengage

12.

All people born in the United States are American

Cengage

All people born in the United States are American

citizens.

Cengage

citizens.

13.

Cengage

13.

14.

Cengage

14.

Learning

If the car does not cost $70,000, it does not go

Learning

If the car does not cost $70,000, it does not go

The car is red and it does not go 140 mph or cost

Learning

The car is red and it does not go 140 mph or cost

Being able to go 140 mph is sufﬁcient for a car to

Learning

Being able to go 140 mph is sufﬁcient for a car to

cost $70,000 or be red.

Learning

cost $70,000 or be red.

Not being red is necessary for a car to cost $70,000

Learning

Not being red is necessary for a car to cost $70,000

and not go 140 mph.

Learning

and not go 140 mph.

In Exercises 11–34, translate the sentence into symbolic form. Be

Learning

In Exercises 11–34, translate the sentence into symbolic form. Be

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

43. What is a negation? 44. What is a conjunction?

45. What is a disjunction? 46. What is a conditional?

47. What is a sufﬁcient condition?

48. What is a necessary condition?

49. What is the difference between the inclusive or and the

exclusive or?

50. Create a sentence that is a self-contradiction, or para-

dox, as in part (e) of Example 1.

•

History Questions

51. In what academic ﬁeld did Gottfried Leibniz receive his

degrees? Why is the study of logic important in this ﬁeld?

52. Who developed a formal system of logic based on syl-

logistic arguments?

53. What is meant by characteristica universalis? Who

proposed this theory?

Exercises 54–58 refer to the following: A culinary institute has a

small restaurant in which the students prepare various dishes.

The menu changes daily, and during a speciﬁc week, the following

dishes are to be prepared: moussaka, pilaf, quiche, ratatouille,

stroganoff, and teriyaki. During the week, the restaurant does

not prepare any other kind of dish. The selection of dishes the

restaurant offers is consistent with the following conditions:

• If the restaurant offers pilaf, then it does not offer ratatouille.

• If the restaurant does not offer stroganoff, then it offers pilaf.

• If the restaurant offers quiche, then it offers both ratatouille and

teriyaki.

• If the restaurant offers teriyaki, then it offers moussaka or

stroganoff or both.

54. Which one of the following could be a complete and

accurate list of the dishes the restaurant offers on a

speciﬁc day?

a. pilaf, quiche, ratatouille, teriyaki

b. quiche, stroganoff, teriyaki

THE NEXT LEVEL

If a person wants to pursue an advanced degree

(something beyond a bachelor’s or four-year

degree), chances are the person must take a stan-

dardized exam to gain admission to a graduate

school or to be admitted into a speciﬁc program.

These exams are intended to measure verbal,

quantitative, and analytical skills that have devel-

oped throughout a person’s life. Many classes and

study guides are available to help people prepare

for the exams. The following questions are typical

of those found in the study guides.

32. If you are rich and famous, you have many friends and

enemies.

33. You get a refund or a store credit if the product is

defective.

34. The streets are slippery if it is raining or snowing.

35. Using the symbolic representations

p: I am an environmentalist.

q: I recycle my aluminum cans.

express the following in words.

a. p ∧ q b. p → q

c. q → p d. q ∨ p

36. Using the symbolic representations

p: I am innocent.

q: I have an alibi.

express the following in words.

a. p ∧ q b. p → q

c. q → p d. q ∨ p

37. Using the symbolic representations

p: I am an environmentalist.

q: I recycle my aluminum cans.

r: I recycle my newspapers.

express the following in words.

a. (q ∨ r) → p b. p → (q ∨ r)

c. (q ∧ r) ∨ p d. (r ∧ q) → p

38. Using the symbolic representations

p: I am innocent.

q: I have an alibi.

r: I go to jail.

express the following in words.

a. (p ∨ q) → r b. (p ∧ q) → r

c. (p ∧ q) ∨ r d. (p ∧ r) → q

39. Which statement, #1 or #2, is more appropriate?

Explain why.

Statement #1: “Cold weather is necessary for it to

snow.”

Statement #2: “Cold weather is sufﬁcient for it to snow.”

40. Which statement, #1 or #2, is more appropriate?

Explain why.

Statement #1: “Being cloudy is necessary for it to rain.”

Statement #2: “Being cloudy is sufﬁcient for it to rain.”

41. Which statement, #1 or #2, is more appropriate?

Explain why.

Statement #1: “Having 31 days in a month is necessary

for it not to be February.”

Statement #2: “Having 31 days in a month is sufﬁcient

for it not to be February.”

42. Which statement, #1 or #2, is more appropriate?

Explain why.

Statement #1: “Being the Fourth of July is necessary

for the U.S. Post Ofﬁce to be closed.”

Statement #2: “Being the Fourth of July is sufﬁcient

for the U.S. Post Ofﬁce to be closed.”

1.2 Exercises 29

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 29

Property

(

Property

(

Property

(p(

Property

(p(

∧

Property

∧

Property

(

Property

(

Property

(p(

Property

(p(

∧

Property

∧

Property

)

Property

)

→

Property

→

Which statement, #1 or #2, is more appropriate?

Property

Which statement, #1 or #2, is more appropriate?

Statement #1: “Cold weather is necessary for it to

Property

Statement #1: “Cold weather is necessary for it to

Statement #2: “Cold weather is sufﬁcient for it to snow.”

Property

Statement #2: “Cold weather is sufﬁcient for it to snow.”

Which statement, #1 or #2, is more appropriate?

Property

Which statement, #1 or #2, is more appropriate?

Explain why.

Property

Explain why.

)

→

Cengage

logistic arguments?

Cengage

logistic arguments?

53.

Cengage

53.

What is meant by

Cengage

What is meant by

proposed this theory?

Cengage

proposed this theory?

Cengage

Learning

Create a sentence that is a self-contradiction, or para-

Learning

Create a sentence that is a self-contradiction, or para-

dox, as in part (e) of Example 1.

Learning

dox, as in part (e) of Example 1.

History Questions

Learning

History Questions

In what academic ﬁeld did Gottfried Leibniz receive his

Learning

In what academic ﬁeld did Gottfried Leibniz receive his

degrees? Why is the study of logic important in this ﬁeld?

Learning

degrees? Why is the study of logic important in this ﬁeld?

Who developed a formal system of logic based on syl-

Learning

Who developed a formal system of logic based on syl-

logistic arguments?

Learning

logistic arguments?

What is meant by

Learning

What is meant by

57. If the restaurant does not offer teriyaki, then which one

of the following must be true?

a. The restaurant offers pilaf.

b. The restaurant offers at most three different dishes.

c. The restaurant offers at least two different dishes.

d. The restaurant offers neither quiche nor ratatouille.

e. The restaurant offers neither quiche nor pilaf.

58. If the restaurant offers teriyaki, then which one of the

following must be false?

a. The restaurant does not offer moussaka.

b. The restaurant does not offer ratatouille.

c. The restaurant does not offer stroganoff.

d. The restaurant offers ratatouille but not quiche.

e. The restaurant offers ratatouille but not stroganoff.

c. quiche, ratatouille, teriyaki

d. ratatouille, stroganoff

e. quiche, ratatouille

55. Which one of the following cannot be a complete and

accurate list of the dishes the restaurant offers on a spe-

ciﬁc day?

a. moussaka, pilaf, quiche, ratatouille, teriyaki

b. quiche, ratatouille, stroganoff, teriyaki

c. moussaka, pilaf, teriyaki

d. stroganoff, teriyaki

e. pilaf, stroganoff

56. Which one of the following could be the only kind of

dish the restaurant offers on a speciﬁc day?

a. teriyaki b. stroganoff

c. ratatouille d. quiche

e. moussaka

30 CHAPTER 1 Logic

1.3 Truth Tables

Objectives

•

Construct a truth table for a compound statement

•

Determine whether two statements are equivalent

•

Apply De Morgan’s Laws

Suppose your friend Maria is a doctor, and you know that she is a Democrat. If

someone told you, “Maria is a doctor and a Republican,” you would say that the

statement was false. On the other hand, if you were told, “Maria is a doctor or a

Republican,” you would say that the statement was true. Each of these state-

ments is a compound statement—the result of joining individual statements

with connective words. When is a compound statement true, and when is it

false? To answer these questions, we must examine whether the individual

statements are true or false and the manner in which the statements are

connected.

The truth value of a statement is the classiﬁcation of the statement as true

or false and is denoted by T or F. For example, the truth value of the statement

“Santa Fe is the capital of New Mexico” is T. (The statement is true.) In contrast,

the truth value of “Memphis is the capital of Tennessee” is F. (The statement is

false.)

A convenient way of determining whether a compound statement is true or

false is to construct a truth table. A truth table is a listing of all possible combina-

tions of the individual statements as true or false, along with the resulting truth

value of the compound statement. As we will see, truth tables also allow us to dis-

tinguish valid arguments from invalid arguments.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 30

Property

Construct a truth table for a compound statement

Property

Construct a truth table for a compound statement

Determine whether two statements are equivalent

Property

Determine whether two statements are equivalent

Apply De Morgan’s Laws

Property

Apply De Morgan’s Laws

Suppose your friend Maria is a doctor, and you know that she is a Democrat. If

Property

Suppose your friend Maria is a doctor, and you know that she is a Democrat. If

someone told you, “Maria is a doctor and a Republican,” you would say that the

Property

someone told you, “Maria is a doctor and a Republican,” you would say that the

statement was false. On the other hand, if you were told, “Maria is a doctor or a

Property

statement was false. On the other hand, if you were told, “Maria is a doctor or a

Construct a truth table for a compound statement

Cengage

Learning

The restaurant does not offer stroganoff.

Learning

The restaurant does not offer stroganoff.

The restaurant offers ratatouille but not quiche.

Learning

The restaurant offers ratatouille but not quiche.

The restaurant offers ratatouille but not stroganoff.

Learning

The restaurant offers ratatouille but not stroganoff.

The Negation p

The negation of a statement is the denial, or opposite, of the statement. (As was

stated in the previous section, because the truth value of the negation depends on the

truth value of the original statement, a negation can be classiﬁed as a compound

statement.) To construct the truth table for the negation of a statement, we must ﬁrst

examine the original statement. A statement p may be true or false, as shown in

Figure 1.31. If the statement p is true, the negation p is false; if p is false, p is

true. The truth table for the compound statement p is given in Figure 1.32. Row 1

of the table is read “p is false when p is true.” Row 2 is read “p is true when

p is false.”

The Conjunction p ∧ q

A conjunction is the joining of two statements with the word and. The compound

statement “Maria is a doctor and a Republican” is a conjunction with the following

symbolic representation:

p: Maria is a doctor.

q: Maria is a Republican.

p ∧ q: Maria is a doctor and a Republican.

The truth value of a compound statement depends on the truth values of the

individual statements that make it up. How many rows will the truth table for the

conjunction p ∧ q contain? Because p has two possible truth values (T or F) and

q has two possible truth values (T or F), we need four (2 · 2) rows in order to list

all possible combinations of Ts and Fs, as shown in Figure 1.33.

For the conjunction p ∧ q to be true, the components p and q must both be

true; the conjunction is false otherwise. The completed truth table for the conjunc-

tion p ∧ q is given in Figure 1.34. The symbols p and q can be replaced by any state-

ments. The table gives the truth value of the statement “p and q,” dependent upon

the truth values of the individual statements “p” and “q.” For instance, row 3 is read

“The conjunction p ∧ q is false when p is false and q is true.” The other rows are

read in a similar manner.

The Disjunction p ∨ q

A disjunction is the joining of two statements with the word or. The compound

statement “Maria is a doctor or a Republican” is a disjunction (the inclusive or)

with the following symbolic representation:

p: Maria is a doctor.

q: Maria is a Republican.

p ∨ q: Maria is a doctor or a Republican.

Even though your friend Maria the doctor is not a Republican, the disjunction

“Maria is a doctor or a Republican” is true. For a disjunction to be true, at least one

of the components must be true. A disjunction is false only when both components

are false. The truth table for the disjunction p ∨ q is given in Figure 1.35.

1.3 Truth Tables 31

Truth values for a statement p.

FIGURE 1.31

Truth table for a negation p.

FIGURE 1.32

p ~p

Truth values for two statements.

FIGURE 1.33

Truth table for a conjunction

p ∧ q.

FIGURE 1.34

pqp∧ q

TT T

TF F

FT F

FF F

Truth table for a disjunction

p ∨ q.

FIGURE 1.35

pqp

∨

TT T

TF T

FT T

FF F

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 31

Property

true; the conjunction is false otherwise. The completed truth table for the conjunc-

Property

true; the conjunction is false otherwise. The completed truth table for the conjunc-

tion

Property

tion

Property

ments. The table gives the truth value of the statement “

Property

ments. The table gives the truth value of the statement “

the truth values of the individual statements “

Property

the truth values of the individual statements “

“The conjunction

Property

“The conjunction

Truth table for a conjunction

Property

Truth table for a conjunction

Property

has two possible truth values (T or F), we need four (2

all possible combinations of Ts and Fs, as shown in Figure 1.33.

For the conjunction

true; the conjunction is false otherwise. The completed truth table for the conjunc-

Cengage

Maria is a Republican.

Cengage

Maria is a Republican.

Maria is a doctor and a Republican.

Cengage

Maria is a doctor and a Republican.

The truth value of a compound statement depends on the truth values of the

Cengage

The truth value of a compound statement depends on the truth values of the

individual statements that make it up. How many rows will the truth table for the

Cengage

individual statements that make it up. How many rows will the truth table for the

conjunction

Cengage

conjunction

Cengage

∧

Cengage

∧

Cengage

contain? Because

Cengage

contain? Because

has two possible truth values (T or F), we need four (2

Cengage

has two possible truth values (T or F), we need four (2

all possible combinations of Ts and Fs, as shown in Figure 1.33.

Cengage

all possible combinations of Ts and Fs, as shown in Figure 1.33.

For the conjunction

Cengage

For the conjunction

Learning

is the joining of two statements with the word

Learning

is the joining of two statements with the word

statement “Maria is a doctor and a Republican” is a conjunction with the following

Learning

statement “Maria is a doctor and a Republican” is a conjunction with the following

EXAMPLE 1 CONSTRUCTING A TRUTH TABLE Under what speciﬁc conditions is the

following compound statement true? “I have a high school diploma, or I have a

full-time job and no high school diploma.”

SOLUTION First, we translate the statement into symbolic form, and then we construct the

truth table for the symbolic expression. Deﬁne p and q as

p: I have a high school diploma.

q: I have a full-time job.

The given statement has the symbolic representation p ∨ (q ∧ p).

Because there are two letters, we need 2  2  4 rows. We need to insert a col-

umn for each connective in the symbolic expression p ∨ (q ∧ p). As in algebra,

we start inside any grouping symbols and work our way out. Therefore, we need a

column for p, a column for q ∧ p, and a column for the entire expression

p ∨ (q ∧ p), as shown in Figure 1.36.

32 CHAPTER 1 Logic

Required columns in the truth table.FIGURE 1.36

pq~pq∧ ~pp∨ (q ∧ ~p)

In the p column, ﬁll in truth values that are opposite those for p. Next, the

conjunction q ∧ p is true only when both components are true; enter a T in row 3

and Fs elsewhere. Finally, the disjunction p ∨ (q ∧ p) is false only when both

components p and (q ∧ p) are false; enter an F in row 4 and Ts elsewhere. The

completed truth table is shown in Figure 1.37.

pq~pq∧ ~pp∨ (q ∧ ~p)

TT F F T

TF F F T

FT T T T

FF T F F

Truth table for p ∨ (q ∧ p).FIGURE 1.37

As is indicated in the truth table, the symbolic expression p ∨ (q ∧ p) is true

under all conditions except one: row 4; the expression is false when both p and q

are false. Therefore, the statement “I have a high school diploma, or I have a full-

time job and no high school diploma” is true in every case except when the speaker

has no high school diploma and no full-time job.

If the symbolic representation of a compound statement consists of two

different letters, its truth table will have 2  2  4 rows. How many rows are re-

quired if a compound statement consists of three letters—say, p, q, and r? Because

each statement has two possible truth values (T and F), the truth table must contain

2  2  2  8 rows. In general, each time a new statement is added, the number of

rows doubles.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 32

Property

completed truth

Property

completed truth

Property

TT F F T

Property

TT F F T

Property

TF F F T

Property

TF F F T

Property

TT F F T

Property

TT F F T

Property

and Fs elsewhere. Finally, the disjunction

components

and (

completed truth

table is shown in Figure 1.37.

Cengage

Required columns in the truth table.

Cengage

Required columns in the truth table.

Cengage

column, ﬁll in truth values that are opposite those for

Cengage

column, ﬁll in truth values that are opposite those for

Cengage

is true only when both components are true; enter a T in row 3

Cengage

is true only when both components are true; enter a T in row 3

and Fs elsewhere. Finally, the disjunction

Cengage

and Fs elsewhere. Finally, the disjunction

Learning



Learning



Learning

). As in algebra,

Learning

). As in algebra,

we start inside any grouping symbols and work our way out. Therefore, we need a

Learning

we start inside any grouping symbols and work our way out. Therefore, we need a

, and a column for the entire expression

Learning

, and a column for the entire expression

Learning

EXAMPLE 2 CONSTRUCTING A TRUTH TABLE Under what speciﬁc conditions is the

following compound statement true? “I own a handgun, and it is not the case that

I am a criminal or police ofﬁcer.”

SOLUTION First, we translate the statement into symbolic form, and then we construct the truth

table for the symbolic expression. Deﬁne the three simple statements as follows:

p: I own a handgun.

q: I am a criminal.

r: I am a police ofﬁcer.

The given statement has the symbolic representation p ∧ (q ∨ r). Since there are

three letters, we need 2

 8 rows. We start with three columns, one for each letter.

To account for all possible combinations of p, q, and r as true or false, proceed as

follows:

1. Fill the ﬁrst half (four rows) of column 1 with Ts and the rest with Fs, as shown in

Figure 1.38(a).

2. In the next column, split each half into halves, the ﬁrst half receiving Ts and the second

Fs. In other words, alternate two Ts and two Fs in column 2, as shown in Fig-

ure 1.38(b).

3. Again, split each half into halves; the ﬁrst half receives Ts, and the second half receives

Fs. Because we are dealing with the third (last) column, the Ts and Fs will alternate, as

shown in Figure 1.38(c).

1.3 Truth Tables 33

pqr

TTT

TTF

TFT

TFF

FTT

FTF

FFT

FFF

(a)

(b)(c)

Truth values for three statements.FIGURE 1.38

(This process of ﬁlling the ﬁrst half of the ﬁrst column with Ts and the second half

with Fs and then splitting each half into halves with blocks of Ts and Fs applies to

all truth tables.)

We need to insert a column for each connective in the symbolic expression

p ∧ (q ∨ r), as shown in Figure 1.39.

NUMBER OF ROWS

If a compound statement consists of n individual statements, each represented

by a different letter, the number of rows required in its truth table is 2

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 33

Property

shown in Figure 1.38(c).

Cengage

Fill the ﬁrst half (four rows) of column 1 with Ts and the rest with Fs, as shown in

Cengage

Fill the ﬁrst half (four rows) of column 1 with Ts and the rest with Fs, as shown in

In the next column, split each half into halves, the ﬁrst half receiving Ts and the second

Cengage

In the next column, split each half into halves, the ﬁrst half receiving Ts and the second

Fs. In other words, alternate two Ts and two Fs in column 2, as shown in Fig-

Cengage

Fs. In other words, alternate two Ts and two Fs in column 2, as shown in Fig-

Again, split each half into halves; the ﬁrst half receives Ts, and the second half receives

Cengage

Again, split each half into halves; the ﬁrst half receives Ts, and the second half receives

Fs. Because we are dealing with the third (last) column, the Ts and Fs will alternate, as

Cengage

Fs. Because we are dealing with the third (last) column, the Ts and Fs will alternate, as

shown in Figure 1.38(c).

Cengage

shown in Figure 1.38(c).

Learning

First, we translate the statement into symbolic form, and then we construct the truth

Learning

First, we translate the statement into symbolic form, and then we construct the truth

table for the symbolic expression. Deﬁne the three simple statements as follows:

Learning

table for the symbolic expression. Deﬁne the three simple statements as follows:

The given statement has the symbolic representation

Learning

The given statement has the symbolic representation

8 rows. We start with three columns, one for each letter.

Learning

8 rows. We start with three columns, one for each letter.

To account for all possible combinations of

Learning

To account for all possible combinations of

p, q,

Learning

p, q,

34 CHAPTER 1 Logic

Required columns in the truth table.FIGURE 1.39

p q r q ∨ r ~(q ∨ r) p ∧ ~(q ∨ r)

TTT

TTF

TFT

TFF

FTT

FTF

FFT

FFF

p q r q ∨ r ~(q ∨ r) p ∧ ~(q ∨ r)

TTT T F F

TTF T F F

TFT T F F

TFF F T T

FTT T F F

FTF T F F

FFT T F F

FFF F T F

p q r q ∨ r ~(q ∨ r) p ∧ ~(q ∨ r)

TTT T F

TTF T F

TFT T F

TFF F T

FTT T F

FTF T F

FFT T F

FFF F T

Truth values of the expressions q ∨ r and ~(q ∨ r).FIGURE 1.40

Truth table for p ∧ (q ∨ r).FIGURE 1.41

Now ﬁll in the appropriate symbol in the column under q ∨ r. Enter F if both

q and r are false; enter T otherwise (that is, if at least one is true). In the (q ∨ r)

column, ﬁll in truth values that are opposite those for q ∨ r, as in Figure 1.40.

The conjunction p ∧ (q ∨ r) is true only when both p and (q ∨ r) are true;

enter a T in row 4 and Fs elsewhere. The truth table is shown in Figure 1.41.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 34

Property

FFT T F

Property

FFT T F

FFF F T

Property

FFF F T

Property

FFT T F

Property

FFT T F

Property

FFF F T

Property

FFF F T

Property

FIGURE 1.40

Property

FIGURE 1.40

enter a T in row 4 and Fs elsewhere. The truth table is shown in Figure 1.41.

Property

enter a T in row 4 and Fs elsewhere. The truth table is shown in Figure 1.41.

Property

FTF T F

FFT T F

FTF T F

FFT T F

Cengage

∨

Cengage

∨

Cengage

)

Cengage

)

Cengage

TTT T F

Cengage

TTT T F

Cengage

TTF T F

Cengage

TTF T F

Cengage

TFT T F

Cengage

TFT T F

Cengage

TFF F T

Cengage

TFF F T

Cengage

FTT T F

Cengage

FTT T F

FTF T F

Cengage

FTF T F

Cengage

TTF T F

Cengage

TTF T F

Cengage

TFT T F

Cengage

TFT T F

TFF F T

Cengage

TFF F T

Cengage

TFF F T

Cengage

TFF F T

Cengage

FTT T F

Cengage

FTT T F

FTF T F

Cengage

FTF T F

Learning

∧

Learning

∧

Learning

Now ﬁll in the appropriate symbol in the column under

Learning

Now ﬁll in the appropriate symbol in the column under

Learning

are false; enter T otherwise (that is, if at least one is true). In the

Learning

are false; enter T otherwise (that is, if at least one is true). In the

column, ﬁll in truth values that are opposite those for

Learning

column, ﬁll in truth values that are opposite those for

Learning

∨

Learning

∨

As indicated in the truth table, the expression p ∧ (q ∨ r) is true only when

p is true and both q and r are false. Therefore, the statement “I own a handgun, and

it is not the case that I am a criminal or police ofﬁcer” is true only when the speaker

owns a handgun, is not a criminal, and is not a police ofﬁcer—in other words, the

speaker is a law-abiding citizen who owns a handgun.

The Conditional p → q

A conditional is a compound statement of the form “If p, then q” and is symbol-

ized p → q. Under what circumstances is a conditional true, and when is it false?

Consider the following (compound) statement: “If you give me $50, then I will give

you a ticket to the ballet.” This statement is a conditional and has the following

representation:

p: You give me $50.

q: I give you a ticket to the ballet.

p → q: If you give me $50, then I will give you a ticket to the ballet.

The conditional can be viewed as a promise: If you give me $50, then I will

give you a ticket to the ballet. Suppose you give me $50; that is, suppose p is true.

I have two options: Either I give you a ticket to the ballet (q is true), or I do not (q is

false). If I do give you the ticket, the conditional p → q is true (I have kept my

promise); if I do not give you the ticket, the conditional p → q is false (I have not

kept my promise). These situations are shown in rows 1 and 2 of the truth table in

Figure 1.42. Rows 3 and 4 require further analysis.

Suppose you do not give me $50; that is, suppose p is false. Whether or not I

give you a ticket, you cannot say that I broke my promise; that is, you cannot say that

the conditional p → q is false. Consequently, since a statement is either true or false,

the conditional is labeled true (by default). In other words, when the premise p of a

conditional is false, it does not matter whether the conclusion q is true or false. In

both cases, the conditional p → q is automatically labeled true, because it is not false.

The completed truth table for a conditional is given in Figure 1.43. Notice

that the only circumstance under which a conditional is false is when the premise

p is true and the conclusion q is false, as shown in row 2.

EXAMPLE 3 CONSTRUCTING A TRUTH TABLE Under what conditions is the symbolic

expression q → p true?

SOLUTION Our truth table has 2

 4 rows and contains a column for p, q, p, and q → p,

as shown in Figure 1.44.

1.3 Truth Tables 35

pqp→ q

TT T

TF F

FT ?

FF ?

What if p is false?

FIGURE 1.42

p q p → q

TT T

TF F

FT T

FF T

Truth table for p → q.

FIGURE 1.43

pq~pq→ ~p

TT F F

TF F T

FT T T

FF T T

Required columns in the

truth table.

FIGURE 1.44

Truth table for q → p.FIGURE 1.45

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 35

Property

both cases, the conditional

Property

both cases, the conditional

The completed truth table for a conditional is given in Figure 1.43. Notice

Property

The completed truth table for a conditional is given in Figure 1.43. Notice

that the only circumstance under which a conditional is false is when the premise

Property

that the only circumstance under which a conditional is false is when the premise

Property

is true and the conclusion

Property

is true and the conclusion

EXAMPLE

Property

EXAMPLE

Property

the conditional is labeled true (by default). In other words, when the premise

conditional is false, it does not matter whether the conclusion

both cases, the conditional

The completed truth table for a conditional is given in Figure 1.43. Notice

Cengage

The conditional can be viewed as a promise:

Cengage

The conditional can be viewed as a promise:

give you a ticket to the ballet. Suppose you give me $50; that is, suppose

Cengage

give you a ticket to the ballet. Suppose you give me $50; that is, suppose

I have two options: Either I give you a ticket to the ballet (

Cengage

I have two options: Either I give you a ticket to the ballet (

false). If I do give you the ticket, the conditional

Cengage

false). If I do give you the ticket, the conditional

promise); if I do not give you the ticket, the conditional

Cengage

promise); if I do not give you the ticket, the conditional

kept my promise). These situations are

Cengage

kept my promise). These situations are

Figure 1.42. Rows 3 and 4 require further analysis.

Cengage

Figure 1.42. Rows 3 and 4 require further analysis.

Suppose you do not give me $50; that is, suppose

Cengage

Suppose you do not give me $50; that is, suppose

give you a ticket, you cannot say that I broke my promise; that is, you cannot say that

Cengage

give you a ticket, you cannot say that I broke my promise; that is, you cannot say that

the conditional

Cengage

the conditional

Cengage

→

Cengage

→

Cengage

the conditional is labeled true (by default). In other words, when the premise

Cengage

the conditional is labeled true (by default). In other words, when the premise

conditional is false, it does not matter whether the conclusion

Cengage

conditional is false, it does not matter whether the conclusion

Learning

Under what circumstances is a conditional true, and when is it false?

Learning

Under what circumstances is a conditional true, and when is it false?

following (compound) statement: “If you give me $50, then I will give

Learning

following (compound) statement: “If you give me $50, then I will give

you a ticket to the ballet.” This statement is a conditional and has the following

Learning

you a ticket to the ballet.” This statement is a conditional and has the following

If you give me $50, then I will give you a ticket to the ballet.

Learning

If you give me $50, then I will give you a ticket to the ballet.

The conditional can be viewed as a promise:

Learning

The conditional can be viewed as a promise:

give you a ticket to the ballet. Suppose you give me $50; that is, suppose

Learning

give you a ticket to the ballet. Suppose you give me $50; that is, suppose

In the p column, ﬁll in truth values that are opposite those for p. Now, a

conditional is false only when its premise (in this case, q) is true and its conclusion

(in this case, p) is false. Therefore, q → p is false only in row 1; the conditional

q → p is true under all conditions except the condition that both p and q are true.

The completed truth table is shown in Figure 1.45.

EXAMPLE 4 CONSTRUCTING A TRUTH TABLE Construct a truth table for the follow-

ing compound statement: “I walk up the stairs if I want to exercise or if the elevator

isn’t working.”

SOLUTION Rewriting the statement so the word if is ﬁrst, we have “If I want to exercise or (if)

the elevator isn’t working, then I walk up the stairs.”

Now we must translate the statement into symbols and construct a truth table.

Deﬁne the following:

p: I want to exercise.

q: The elevator is working.

r: I walk up the stairs.

The statement now has the symbolic representation (p ∨ q) → r. Because we

have three letters, our table must have 2

 8 rows. Inserting a column for each

letter and a column for each connective, we have the initial setup shown in

Figure 1.46.

36 CHAPTER 1 Logic

pqr~q p ∨ ~q (p ∨ ~q) → r

TTT

TTF

TFT

TFF

FTT

FTF

FFT

FFF

Required columns in the truth table.FIGURE 1.46

In the column labeled q, enter truth values that are the opposite of those

of q. Next, enter the truth values of the disjunction p ∨ q in column 5. Recall that

a disjunction is false only when both components are false and is true otherwise.

Consequently, enter Fs in rows 5 and 6 (since both p and q are false) and Ts in

the remaining rows, as shown in Figure 1.47.

The last column involves a conditional; it is false only when its premise is true

and its conclusion is false. Therefore, enter Fs in rows 2, 4, and 8 (since p ∨ q is

true and r is false) and Ts in the remaining rows. The truth table is shown in

Figure 1.48.

As Figure 1.48 shows, the statement “I walk up the stairs if I want to exercise

or if the elevator isn’t working” is true in all situations except those listed in rows

2, 4, and 8. For instance, the statement is false (row 8) when the speaker does not

want to exercise, the elevator is not working, and the speaker does not walk up the

stairs—in other words, the speaker stays on the ground ﬂoor of the building when

the elevator is broken.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 36

Property

TFF

Property

TFF

Property

FTT

Property

FTT

Property

FTF

Property

FTF

Property

FFT

Property

FFT

Property

TFF

Property

TFF

Property

FTT

Property

FTT

Property

FTF

Property

FTF

Property

TFT

TFF

TFT

TFF

Cengage

The statement now has the symbolic representation (

Cengage

The statement now has the symbolic representation (

have three letters, our table must have 2

Cengage

have three letters, our table must have 2

Cengage



Cengage



8 rows. Inserting a column for each

Cengage

8 rows. Inserting a column for each

letter and a column for each connective, we have the initial setup shown in

Cengage

letter and a column for each connective, we have the initial setup shown in

Cengage

q p

Cengage

q p

∨

Cengage

∨

Cengage

TTF

Cengage

TTF

Cengage

q p

Cengage

q p

Cengage

Learning

is ﬁrst, we have “If I want to exercise or (if)

Learning

is ﬁrst, we have “If I want to exercise or (if)

Now we must translate the statement into symbols and construct a truth table.

Learning

Now we must translate the statement into symbols and construct a truth table.

The statement now has the symbolic representation (

Learning

The statement now has the symbolic representation (

1.3 Truth Tables 37

Equivalent Expressions

When you purchase a car, the car is either new or used. If a salesperson told you,

“It is not the case that the car is not new,” what condition would the car be in? This

compound statement consists of one individual statement (“p: The car is new”) and

two negations:

“It is not the case that the car is not new.”

p

Does this mean that the car is new? To answer this question, we will construct a

truth table for the symbolic expression (p) and compare its truth values with

those of the original p. Because there is only one letter, we need 2

 2 rows, as

shown in Figure 1.49.

We must insert a column for p and a column for (p). Now, p has truth

values that are opposite those of p, and (p) has truth values that are opposite

those of p, as shown in Figure 1.50.

↑↑↑↑

pqr~q p ∨ ~q (p ∨ ~q) → r

TTT F T

TTF F T

TFT T T

TFF T T

FTT F F

FTF F F

FFT T T

FFF T T

Truth values of the expressions.FIGURE 1.47

Truth table for (p ∨ q) → r.FIGURE 1.48

pqr~q p ∨ ~q (p ∨ ~q) → r

TTT F T T

TTF F T F

TFT T T T

TFF T T F

FTT F F T

FTF F F T

FFT T T T

FFF T T F

Truth values of p.

FIGURE 1.49

Truth table for (p).

FIGURE 1.50

p ~p ~(~p)

TF T

FT F

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 37

Property

FIGURE 1.48

FFF T T F

Cengage

TTF F T F

Cengage

TTF F T F

Cengage

TFT T T T

Cengage

TFT T T T

Cengage

TFF T T F

Cengage

TFF T T F

Cengage

FTT F F T

Cengage

FTT F F T

Cengage

FTF F F T

Cengage

FTF F F T

Cengage

FFT T T T

Cengage

FFT T T T

FFF T T F

Cengage

FFF T T F

Cengage

TFT T T T

Cengage

TFT T T T

Cengage

TFF T T F

Cengage

TFF T T F

FTT F F T

Cengage

FTT F F T

Cengage

TFF T T F

Cengage

TFF T T F

Cengage

FTT F F T

Cengage

FTT F F T

Cengage

FTF F F T

Cengage

FTF F F T

Cengage

FTF F F T

Cengage

FTF F F T

Cengage

FFT T T T

Cengage

FFT T T T

FFF T T F

Cengage

FFF T T F

Learning

(

Learning

(

Learning

∨

Learning

∨

Learning

)

Learning

)

Learning

TTT F T T

Learning

TTT F T T

TTF F T F

Learning

TTF F T F

Learning

TTT F T T

Learning

TTT F T T

TTF F T F

Learning

TTF F T F

Notice that the values in the column labeled (p) are identical to those in

the column labeled p. Whenever this happens, the expressions are said to be

equivalent and may be used interchangeably. Therefore, the statement “It is not

the case that the car is not new” is equivalent in meaning to the statement “The

car is new.”

Equivalent expressions are symbolic expressions that have identical truth

values in each corresponding entry. The expression p  q is read “p is equiva-

lent to q” or “p and q are equivalent.” As we can see in Figure 1.50, an expres-

sion and its double negation are logically equivalent. This relationship can be

expressed as p (p).

EXAMPLE 5 DETERMINING WHETHER STATEMENTS ARE EQUIVALENT Are the

statements “If I am a homeowner, then I pay property taxes” and “I am a

homeowner, and I do not pay property taxes” equivalent?

SOLUTION We begin by deﬁning the statements:

p: I am a homeowner.

q: I pay property taxes.

p → q: If I am a homeowner, then I pay property taxes.

p ∧ q: I am a homeowner, and I do not pay property taxes.

The truth table contains 2

 4 rows, and the initial setup is shown in Figure 1.51.

Now enter the appropriate truth values under q (the opposite of q). Because

the conjunction p ∧ q is true only when both p and q are true, enter a T in row 2

and Fs elsewhere. The conditional p → q is false only when p is true and q is false;

therefore, enter an F in row 2 and Ts elsewhere. The completed truth table is shown

in Figure 1.52.

Because the entries in the columns labeled p ∧ q and p → q are not the

same, the statements are not equivalent. “If I am a homeowner, then I pay

property taxes” is not equivalent to “I am a homeowner and I do not pay property

taxes.”

38 CHAPTER 1 Logic

pq~q p ∧ ~q p → q

Required columns in the

truth table.

FIGURE 1.51

pq~q p ∧ ~q p → q

TTF F T

TFT T F

FTF F T

FFT F T

Truth table for p → q.FIGURE 1.52

Notice that the truth values in the columns under p ∧ q and p → q in Fig-

ure 1.52 are exact opposites; when one is T, the other is F. Whenever this happens,

one statement is the negation of the other. Consequently, p ∧ q is the negation of

p → q (and vice versa). This can be expressed as p ∧ q (p → q). The nega-

tion of a conditional is logically equivalent to the conjunction of the premise and the

negation of the conclusion.

Statements that look or sound different may in fact have the same meaning. For

example, “It is not the case that the car is not new” really means the same as “Thecar

is new,” and “It is not the case that if I am a homeowner, then I pay property taxes”

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 38

Property

same, the statements are not equivalent. “If I am a homeowner, then I pay

property taxes” is

not

Cengage

If I am a homeowner, then I pay property taxes.

Cengage

If I am a homeowner, then I pay property taxes.

I am a homeowner, and I do not pay property taxes.

Cengage

I am a homeowner, and I do not pay property taxes.

4 rows, and the initial setup is shown in Figure 1.51.

Cengage

4 rows, and the initial setup is shown in Figure 1.51.

Now enter the appropriate truth values under

Cengage

Now enter the appropriate truth values under

is true only when both

Cengage

is true only when both

and Fs elsewhere. The conditional

Cengage

and Fs elsewhere. The conditional

Cengage

→

Cengage

→

therefore, enter an F in row 2 and Ts elsewhere. The completed truth table is shown

Cengage

therefore, enter an F in row 2 and Ts elsewhere. The completed truth table is shown

Because the entries in the columns labeled

Cengage

Because the entries in the columns labeled

same, the statements are not equivalent. “If I am a homeowner, then I pay

Cengage

same, the statements are not equivalent. “If I am a homeowner, then I pay

equivalent to “I am a homeowner and I do not pay property

Cengage

equivalent to “I am a homeowner and I do not pay property

Learning

DETERMINING WHETHER STATEMENTS ARE EQUIVALENT

Learning

DETERMINING WHETHER STATEMENTS ARE EQUIVALENT

statements “If I am a homeowner, then I pay property taxes” and “I am a

Learning

statements “If I am a homeowner, then I pay property taxes” and “I am a

If I am a homeowner, then I pay property taxes.

Learning

If I am a homeowner, then I pay property taxes.

I am a homeowner, and I do not pay property taxes.

Learning

I am a homeowner, and I do not pay property taxes.

1.3 Truth Tables 39

GEORGE BOOLE, 1815–1864

Boole’s most inﬂuen-

tial work, An Investiga-

tion of the Laws of

Thought, on Which Are

Founded the Mathe-

matical Theories of

Logic and Probabilities,

was published in

1854. In it, he wrote,

“There exist certain

general principles founded in the very na-

ture of language and logic that exhibit

laws as identical in form as with the laws

of the general symbols of algebra.” With

this insight, Boole had taken a big step

into the world of logical reasoning and

abstract mathematical analysis.

Perhaps because of his lack of formal

training, Boole challenged the status quo,

including the Aristotelian assumption that

all logical arguments could be reduced

to syllogistic arguments. In doing so, he

employed symbols to represent concepts,

as did Leibniz, but he also developed

systems of algebraic manipulation to ac-

company these symbols. Thus, Boole’s

creation is a marriage of logic and math-

ematics. However, as is the case with al-

most all new theories, Boole’s symbolic

logic was not met with total approbation.

In particular, one staunch opponent of his

work was Georg Cantor, whose work on

the origins of set theory and the magni-

tude of inﬁnity will be investigated in

Chapter 2.

In the many years since Boole’s

original work was unveiled, various

scholars have modiﬁed, improved, gen-

eralized, and extended its central con-

cepts. Today, Boolean algebras are the

essence of computer software and cir-

cuit design. After all, a computer merely

manipulates predeﬁned symbols and

conforms to a set of preassigned alge-

braic commands.

Historical

Note

Through an algebraic manipulation of logical

symbols, Boole revolutionized the age-old study of

logic. His essay The Mathematical Analysis of

Logic laid the foundation for his later book

An Investigation of the Laws of Thought.

Brown University Library

eorge Boole is called “the

father of symbolic logic.”

Computer science owes much

to this self-educated mathemati-

cian. Born the son of a poor

shopkeeper in Lincoln, Eng-

land, Boole had very little for-

mal education, and his prospects for ris-

ing above his family’s lower-class status

were dim. Like Leibniz, he taught himself

Latin; at the age of twelve, he translated

an ode of Horace into English, winning

the attention of the local schoolmasters.

(In his day, knowledge of Latin was a

prerequisite to scholarly endeavors and

to becoming a socially accepted gentle-

man.) After that, his academic desires

were encouraged, and at the age of ﬁf-

teen, he began his long teaching ca-

reer. While teaching arithmetic, he stud-

ied advanced mathematics and physics.

In 1849, after nineteen years of

teaching at elementary schools, Boole

received his big break: He was ap-

pointed professor of mathematics at

Queen’s College in the city of Cork,

Ireland. At last, he was able to research

advanced mathematics, and he be-

came recognized as a ﬁrst-class mathe-

matician. This was a remarkable feat,

considering Boole’s lack of formal train-

ing and degrees.

actually means the same as “I am a homeowner, and I do not pay property taxes.”

When we are working with equivalent statements, we can substitute either state-

ment for the other without changing the truth value.

De Morgan’s Laws

Earlier in this section, we saw that the negation of a negation is equivalent to the

original statement; that is, (p)  p. Another negation “formula” that we dis-

covered was (p → q)  p ∧ q, that is, the negation of a conditional. Can we

ﬁnd similar “formulas” for the negations of the other basic connectives, namely,

the conjunction and the disjunction? The answer is yes, and the results are credited

to the English mathematician and logician Augustus De Morgan.

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 39

Property

advanced mathematics, and he be-

Property

advanced mathematics, and he be-

came recognized as a ﬁrst-class mathe-

Property

came recognized as a ﬁrst-class mathe-

matician. This was a remarkable feat,

Property

matician. This was a remarkable feat,

considering Boole’s lack of formal train-

Property

considering Boole’s lack of formal train-

Property

ematics. However, as is the case with al-

most all new theories, Boole’s symbolic

logic was not met with total approbation.

In particular, one staunch opponent of his

Ireland. At last, he was able to research

Cengage

Perhaps because of his lack of formal

Cengage

Perhaps because of his lack of formal

training, Boole challenged the status quo,

Cengage

training, Boole challenged the status quo,

including the Aristotelian assumption that

Cengage

including the Aristotelian assumption that

logical arguments could be reduced

Cengage

logical arguments could be reduced

to syllogistic arguments. In doing so, he

Cengage

to syllogistic arguments. In doing so, he

employed symbols to represent concepts,

Cengage

employed symbols to represent concepts,

as did Leibniz, but he also developed

Cengage

as did Leibniz, but he also developed

systems of algebraic manipulation to ac-

Cengage

systems of algebraic manipulation to ac-

company these symbols. Thus, Boole’s

Cengage

company these symbols. Thus, Boole’s

creation is a marriage of logic and math-

Cengage

creation is a marriage of logic and math-

ematics. However, as is the case with al-

Cengage

ematics. However, as is the case with al-

most all new theories, Boole’s symbolic

Cengage

most all new theories, Boole’s symbolic

Learning

this insight, Boole had taken a big step

Learning

this insight, Boole had taken a big step

into the world of logical reasoning and

Learning

into the world of logical reasoning and

Perhaps because of his lack of formal

Learning

Perhaps because of his lack of formal

training, Boole challenged the status quo,

Learning

training, Boole challenged the status quo,

manipulates predeﬁned symbols and

Learning

manipulates predeﬁned symbols and

conforms to a set of preassigned alge-

Learning

conforms to a set of preassigned alge-

braic commands.

Learning

braic commands.

Learning

40 CHAPTER 1 Logic

p ~p

pqp∧ q

TT T

TF F

FT F

FF F

pqp∨ q

TT T

TF T

FT T

FF F

p qp→ q

TT T

TF F

FT T

FF T

Negation

Conjunction Disjunction Conditional

Truth tables for the basic connectives.FIGURE 1.53

De Morgan’s Laws are easily veriﬁed through the use of truth tables and will

be addressed in the exercises (see Exercises 55 and 56).

EXAMPLE 6 APPLYING D

E MORGAN’S LAWS Using De Morgan’s Laws, ﬁnd the negation

of each of the following:

a. It is Friday and I receive a paycheck.

b. You are correct or I am crazy.

SOLUTION a. The symbolic representation of “It is Friday and I receive a paycheck” is

p: It is Friday.

q: I receive a paycheck.

p ∧ q: It is Friday and I receive a paycheck.

Therefore, the negation is (p ∧ q) p ∨ q, that is, “It is not Friday or I do not re-

ceive a paycheck.”

b. The symbolic representation of “You are correct or I am crazy” is

p: You are correct.

q: I am crazy.

p ∨ q: You are correct or I am crazy.

Therefore, the negation is (p ∨ q) p ∧ q, that is, “You are not correct and I am

not crazy.”

As we have seen, the truth value of a compound statement depends on the

truth values of the individual statements that make it up. The truth tables of the

basic connectives are summarized in Figure 1.53.

Equivalent statements are statements that have the same meaning. Equivalent

statements for the negations of the basic connectives are given in Figure 1.54.

DE MORGAN’S LAWS

The negation of the conjunction p ∧ q is given by (p ∧ q) p ∨ q.

“Not p and q” is equivalent to “not p or not q.”

The negation of the disjunction p ∨ q is given by (p ∨ q) p ∧ q.

“Not p or q” is equivalent to “not p and not q.”

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 40

Property

∨

Property

∨

Property

Therefore, the negation is

Property

Therefore, the negation is

not crazy.”

Property

not crazy.”

truth values of the individual statements that make it up. The truth tables of the

Property

truth values of the individual statements that make it up. The truth tables of the

Property

You are correct.

I am crazy.

You are correct or I am crazy.

Cengage

The symbolic representation of “It is Friday and I receive a paycheck” is

Cengage

The symbolic representation of “It is Friday and I receive a paycheck” is

It is Friday and I receive a paycheck.

Cengage

It is Friday and I receive a paycheck.

Therefore, the negation is

Cengage

Therefore, the negation is



Cengage



(

Cengage

(

Cengage

∧

Cengage

∧

Cengage

)

Cengage

)

The symbolic representation of “You are correct or I am crazy” is

Cengage

The symbolic representation of “You are correct or I am crazy” is

You are correct.

Cengage

You are correct.

Learning

De Morgan’s Laws are easily veriﬁed through the use of truth tables and will

Learning

De Morgan’s Laws are easily veriﬁed through the use of truth tables and will

Using De Morgan’s Laws, ﬁnd the negation

Learning

Using De Morgan’s Laws, ﬁnd the negation

The symbolic representation of “It is Friday and I receive a paycheck” is

Learning

The symbolic representation of “It is Friday and I receive a paycheck” is

1.3 Exercises 41

1. ~(~p) ≡ p the negation of a negation

2. ~(p ∧ q) ≡ ~p ∨ ~q the negation of a conjunction

3. ~(p ∨ q) ≡ ~p ∧ ~q the negation of a disjunction

4. ~(p → q) ≡ p ∧ ~q the negation of a conditional

Negations of the basic connectives.FIGURE 1.54

1.3

Exercises

In Exercises 1–20, construct a truth table for the symbolic

expressions.

1. p ∨ q

2. p ∧ q

3. p ∨ p

4. p ∧ p

5. p → q

6. p → q

7. q → p

8. p → q

9. (p ∨ q) → p

10. (p ∧ q) → q

11. (p ∨ q) → (p ∧ q)

12. (p ∧ q) → (p ∨ q)

13. p ∧ (q ∨ r)

14. p ∨ (q ∨ r)

15. p ∨ (q ∧ r)

16. p ∨ (q ∧ r)

17. (r ∨ p) → (q ∧ p)

18. (q ∧ p) → (r ∨ p)

19. (p ∨ r) → (q ∧ r)

20. (p ∧ r) → (q ∨ r)

In Exercises 21–40, translate the compound statement into

symbolic form and then construct the truth table for the

expression.

21. If it is raining, then the streets are wet.

22. If the lyrics are not controversial, the performance is

not banned.

23. The water supply is rationed if it does not rain.

24. The country is in trouble if he is elected.

25. All squares are rectangles.

26. All muscle cars from the Sixties are polluters.

27. No square is a triangle.

28. No electric-powered car is a polluter.

29. Being a monkey is sufﬁcient for not being an ape.

30. Being a chimpanzee is sufﬁcient for not being a monkey.

31. Not being a monkey is necessary for being an ape.

32. Not being a chimpanzee is necessary for being a monkey.

33. Your check is accepted if you have a driver’s license or

a credit card.

34. Yougetarefundorastorecreditiftheproductisdefective.

35. If leaded gasoline is used, the catalytic converter is

damaged and the air is polluted.

36. If he does not go to jail, he is innocent or has an alibi.

37. I have a college degree and I do not have a job or own

a house.

38. I surf the Internet and I make purchases and do not pay

sales tax.

39. If Proposition A passes and Proposition B does not,

jobs are lost or new taxes are imposed.

40. If Proposition A does not pass and the legislature raises

taxes, the quality of education is lowered and unem-

ployment rises.

In Exercises 41–50, construct a truth table to determine whether

the statements in each pair are equivalent.

41. The streets are wet or it is not raining.

If it is raining, then the streets are wet.

42. The streets are wet or it is not raining.

If the streets are not wet, then it is not raining.

43. He has a high school diploma or he is unemployed.

If he does not have a high school diploma, then he is

unemployed.

44. She is unemployed or she does not have a high school

diploma.

If she is employed, then she does not have a high

school diploma.

45. If handguns are outlawed, then outlaws have handguns.

If outlaws have handguns, then handguns are outlawed.

46. If interest rates continue to fall, then I can afford to buy

a house.

If interest rates do not continue to fall, then I cannot

afford to buy a house.

47. If the spotted owl is on the endangered species list,

then lumber jobs are lost.

95057_01_ch01_p001-066.qxd 9/28/10 4:36 PM Page 41

Property

)

Property

)

∨

Property

∨

Property

)

Property

)

(

Property

(

Property

∧

Property

∧



Property



Property

)

Property

)

→

Property

→

(

Property

(

Property

∨

Property

∨



Property



Property

)

Property

)

In Exercises 21–40, translate the compound statement into

Property

In Exercises 21–40, translate the compound statement into

Cengage

Yougetarefundorastorecreditiftheproductisdefective.

Cengage

Yougetarefundorastorecreditiftheproductisdefective.

35.

Cengage

35.

If leaded gasoline is used, the catalytic converter is

Cengage

If leaded gasoline is used, the catalytic converter is

damaged and the air is polluted.

Cengage

damaged and the air is polluted.

36.

Cengage

36.

If he does not go to jail, he is innocent or has an alibi.

Cengage

If he does not go to jail, he is innocent or has an alibi.

37.

Cengage

37.

I have a college degree and I do not have a job or own

Cengage

I have a college degree and I do not have a job or own

Learning

Being a chimpanzee is sufﬁcient for not being a monkey.

Learning

Being a chimpanzee is sufﬁcient for not being a monkey.

Not being a monkey is necessary for being an ape.

Learning

Not being a monkey is necessary for being an ape.

Not being a chimpanzee is necessary for being a monkey.

Learning

Not being a chimpanzee is necessary for being a monkey.

Your check is accepted if you have a driver’s license or

Learning

Your check is accepted if you have a driver’s license or

a credit card.

Learning

a credit card.

Yougetarefundorastorecreditiftheproductisdefective.

Learning

Yougetarefundorastorecreditiftheproductisdefective.

If leaded gasoline is used, the catalytic converter is

Learning

If leaded gasoline is used, the catalytic converter is

In Exercises 57–68, write the statement in symbolic form,

construct the negation of the expression (in simpliﬁed symbolic

form), and express the negation in words.

57. I have a college degree and I am not employed.

58. It is snowing and classes are canceled.

59. The television set is broken or there is a power outage.

60. The freeway is under construction or I do not ride

the bus.

61. If the building contains asbestos, the original contrac-

tor is responsible.

62. If the legislation is approved, the public is uninformed.

63. The First Amendment has been violated if the lyrics

are censored.

64. Your driver’s license is taken away if you do not obey

the laws.

65. Rainy weather is sufﬁcient for not washing my car.

66. Drinking caffeinated coffee is sufﬁcient for not

sleeping.

67. Not talking is necessary for listening.

68. Not eating dessert is necessary for being on a diet.

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

69. a. Under what conditions is a disjunction true?

b. Under what conditions is a disjunction false?

70. a. Under what conditions is a conjunction true?

b. Under what conditions is a conjunction false?

71. a. Under what conditions is a conditional true?

b. Under what conditions is a conditional false?

72. a. Under what conditions is a negation true?

b. Under what conditions is a negation false?

73. What are equivalent expressions?

74. What is a truth table?

75. When constructing a truth table, how do you determine

how many rows to create?

•

History Questions

76. Who is considered “the father of symbolic logic”?

77. Boolean algebra is a combination of logic and math-

ematics. What is it used for?

If lumber jobs are not lost, then the spotted owl is not

on the endangered species list.

48. If I drink decaffeinated coffee, then I do not stay

awake.

If I do stay awake, then I do not drink decaffeinated

coffee.

49. The plaintiff is innocent or the insurance company

does not settle out of court.

The insurance company settles out of court and the

plaintiff is not innocent.

50. The plaintiff is not innocent and the insurance com-

pany settles out of court.

It is not the case that the plaintiff is innocent or the in-

surance company does not settle out of court.

In Exercises 51–54, construct truth tables to determine which

pairs of statements are equivalent.

51. i. Knowing Morse code is sufﬁcient for operating a

telegraph.

ii. Knowing Morse code is necessary for operating a

telegraph.

iii. Not knowing Morse code is sufﬁcient for not

operating a telegraph.

iv. Not knowing Morse code is necessary for not

operating a telegraph.

52. i. Knowing CPR is necessary for being a paramedic.

ii. Knowing CPR is sufﬁcient for being a paramedic.

iii. Not knowing CPR is necessary for not being a

paramedic.

iv. Not knowing CPR is sufﬁcient for not being a

paramedic.

53. i. The water being cold is necessary for not going

swimming.

ii. The water not being cold is necessary for going

swimming.

iii. The water being cold is sufﬁcient for not going

swimming.

iv. The water not being cold is sufﬁcient for going

swimming.

54. i. The sky not being clear is sufﬁcient for it to be

raining.

ii. The sky being clear is sufﬁcient for it not to be

raining.

iii. Thesky notbeingclearisnecessaryforit toberaining.

iv. Theskybeingclearisnecessaryforitnottoberaining.

55. Using truth tables, verify De Morgan’s Law

(p ∧ q) p ∨ q.

56. Using truth tables, verify De Morgan’s Law

(p ∨ q) p ∧ q.

42 CHAPTER 1 Logic

95057_01_ch01_p001-066.qxd 9/27/10 9:34 AM Page 42

Property

The water being cold is necessary for not going

Property

The water being cold is necessary for not going

The water not being cold is necessary for going

Property

The water not being cold is necessary for going

The water being cold is sufﬁcient for not going

Property

The water being cold is sufﬁcient for not going

The water not being cold is sufﬁcient for going

Property

The water not being cold is sufﬁcient for going

The sky not being clear is sufﬁcient for it to be

Property

The sky not being clear is sufﬁcient for it to be

Not knowing CPR is sufﬁcient for not being a

The water being cold is necessary for not going

Cengage

Not eating dessert is necessary for being on a diet.

Cengage

Not eating dessert is necessary for being on a diet.

Answer the following questions using complete

Cengage

Answer the following questions using complete

sentences and your own words.

Cengage

sentences and your own words.

•

Cengage

•

Concept Questions

Cengage

Concept Questions

69. a.

Cengage

69. a.

Not knowing CPR is necessary for not being a

Cengage

Not knowing CPR is necessary for not being a

Not knowing CPR is sufﬁcient for not being a

Cengage

Not knowing CPR is sufﬁcient for not being a

Cengage

Learning

The First Amendment has been violated if the lyrics

Learning

The First Amendment has been violated if the lyrics

Your driver’s license is taken away if you do not obey

Learning

Your driver’s license is taken away if you do not obey

Rainy weather is sufﬁcient for not washing my car.

Learning

Rainy weather is sufﬁcient for not washing my car.

Drinking caffeinated coffee is sufﬁcient for not

Learning

Drinking caffeinated coffee is sufﬁcient for not

Not talking is necessary for listening.

Learning

Not talking is necessary for listening.

Not eating dessert is necessary for being on a diet.

Learning

Not eating dessert is necessary for being on a diet.

1.4 More on Conditionals

Objectives

•

Create the converse, inverse, and contrapositive of a conditional statement

•

Determine equivalent variations of a conditional statement

•

Interpret “only if” statements

•

Interpret a biconditional statement

Conditionals differ from conjunctions and disjunctions with regard to the possibil-

ity of changing the order of the statements. In algebra, the sum x  y is equal to the

sum y  x; that is, addition is commutative. In everyday language, one realtor might

say, “The house is perfect and the lot is priceless,” while another says, “The lot is

priceless and the house is perfect.” Logically, their meanings are the same, since

(p ∧ q)  (q ∧ p). The order of the components in a conjunction or disjunction makes

no difference in regard to the truth value of the statement. This is not so with

conditionals.

Variations of a Conditional

Given two statements p and q, various “if . . . then . . .” statements can be formed.

EXAMPLE 1 TRANSLATING SYMBOLS INTO WORDS Using the statements

p: You are compassionate.

q: You contribute to charities.

write an “if . . . then . . .” sentence represented by each of the following:

a. p → q b. q → p c. p → q d. q → p

SOLUTION a. p → q: If you are compassionate, then you contribute to charities.

b. q → p: If you contribute to charities, then you are compassionate.

c. p → q: If you are not compassionate, then you do not contribute to charities.

d. q → p: If you do not contribute to charities, then you are not compassionate.

Each part of Example 1 contains an “if . . . then . . .” statement and is called

a conditional. Any given conditional has three variations: a converse, an inverse,

and a contrapositive. The converse of the conditional “if p then q” is the com-

pound statement “if q then p” That is, we form the converse of the conditional by

interchanging the premise and the conclusion; q → p is the converse of p → q. The

statement in part (b) of Example 1 is the converse of the statement in part (a).

The inverse of the conditional “if p then q” is the compound statement “if not

p then not q.” We form the inverse of the conditional by negating both the premise

and the conclusion; p → q is the inverse of p → q. The statement in part (c) of

Example 1 is the inverse of the statement in part (a).

The contrapositive of the conditional “if p then q” is the compound

statement “if not q then not p.” We form the contrapositive of the conditional by

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 43

Property

write an “if . . . then . . .” sentence represented by each of the following:

Property

write an “if . . . then . . .” sentence represented by each of the following:

SOLUTION

Property

SOLUTION

Property

TRANSLATING SYMBOLS INTO WORDS

You are compassionate.

Cengage

the truth value of the statement. This is not so with

Cengage

the truth value of the statement. This is not so with

Variations of a Conditional

Cengage

Variations of a Conditional

Given two statements

Cengage

Given two statements

Cengage

TRANSLATING SYMBOLS INTO WORDS

Cengage

TRANSLATING SYMBOLS INTO WORDS

Learning

Conditionals differ from conjunctions and disjunctions with regard to the possibil-

Learning

Conditionals differ from conjunctions and disjunctions with regard to the possibil-

ity of changing the order of the statements. In algebra, the sum

Learning

ity of changing the order of the statements. In algebra, the sum

; that is, addition is commutative. In everyday language, one realtor might

Learning

; that is, addition is commutative. In everyday language, one realtor might

say, “The house is perfect and the lot is priceless,” while another says, “The lot is

Learning

say, “The house is perfect and the lot is priceless,” while another says, “The lot is

is perfect.” Logically, their meanings are the same, since

Learning

is perfect.” Logically, their meanings are the same, since

). The order of the components in a conjunction or disjunction makes

Learning

). The order of the components in a conjunction or disjunction makes

the truth value of the statement. This is not so with

Learning

the truth value of the statement. This is not so with

negating and interchanging both the premise and the conclusion; q → p is the

contrapositive of p → q. The statement in part (d) of Example 1 is the contraposi-

tive of the statement in part (a). The variations of a given conditional are summa-

rized in Figure 1.55. As we will see, some of these variations are equivalent, and

some are not. Unfortunately, many people incorrectly treat them all as equivalent.

44 CHAPTER 1 Logic

Variations of a conditional.FIGURE 1.55

Name Symbolic Form Read As . . .

a (given) conditional p → q If p, then q.

the converse (of p → q) q → p If q, then p.

the inverse (of p → q)~p → ~q If not p, then not q.

the contrapositive (of p → q)~q → ~p If not q, then not p.

EXAMPLE 2 CREATING VARIATIONS OFACONDITIONALSTATEMENT Given the

conditional “You did not receive the proper refund if you prepared your own

income tax form,” write the sentence that represents each of the following.

a. the converse of the conditional

b. the inverse of the conditional

c. the contrapositive of the conditional

SOLUTION a. Rewriting the statement in the standard “if . . . then . . .” form, we have the conditional

“If you prepared your own income tax form, then you did not receive the proper re-

fund.” The converse is formed by interchanging the premise and the conclusion. Thus,

the converse is written as “If you did not receive the proper refund, then you prepared

your own income tax form.”

b. The inverse is formed by negating both the premise and the conclusion. Thus, the in-

verse is written as “If you did not prepare your own income tax form, then you received

the proper refund.”

c. The contrapositive is formed by negating and interchanging the premise and the con-

clusion. Thus, the contrapositive is written as “If you received the proper refund, then

you did not prepare your own income tax form.”

Equivalent Conditionals

We have seen that the conditional p → q has three variations: the converse q → p, the

inverse p → q, and the contrapositive q → p. Do any of these “if . . . then . . .”

statements convey the same meaning? In other words, are any of these compound

statements equivalent?

EXAMPLE 3 DETERMINING EQUIVALENT STATEMENTS Determine which (if any)

of the following are equivalent: a conditional p → q, the converse q → p, the

inverse p → q, and the contrapositive q → p.

SOLUTION To investigate the possible equivalencies, we must construct a truth table that con-

tains all the statements. Because there are two letters, we need 2

 4 rows. The

table must have a column for p, one for q, one for the conditional p → q, and

one for each variation of the conditional. The truth values of the negations p and

q are readily entered, as shown in Figure 1.56.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 44

Property

the proper refund.”

Property

the proper refund.”

The contrapositive is formed by negating

Property

The contrapositive is formed by negating

clusion. Thus, the contrapositive is written as “If you received the proper refund, then

Property

clusion. Thus, the contrapositive is written as “If you received the proper refund, then

you did not prepare your own income tax form.”

Property

you did not prepare your own income tax form.”

Equivalent Conditionals

Property

Equivalent Conditionals

The inverse is formed by negating both the premise and the conclusion. Thus, the in-

verse is written as “If you did not prepare your own income tax form, then you received

the proper refund.”

The contrapositive is formed by negating

Cengage

the contrapositive of the conditional

Cengage

the contrapositive of the conditional

Rewriting the statement in the standard “if . . . then . . .” form, we have the conditional

Cengage

Rewriting the statement in the standard “if . . . then . . .” form, we have the conditional

“If you prepared your own income tax form, then you did not receive the proper re-

Cengage

“If you prepared your own income tax form, then you did not receive the proper re-

fund.” The converse is formed by interchanging the premise and the conclusion. Thus,

Cengage

fund.” The converse is formed by interchanging the premise and the conclusion. Thus,

the converse is written as “If you did not receive the proper refund, then you prepared

Cengage

the converse is written as “If you did not receive the proper refund, then you prepared

your own income tax form.”

Cengage

your own income tax form.”

The inverse is formed by negating both the premise and the conclusion. Thus, the in-

Cengage

The inverse is formed by negating both the premise and the conclusion. Thus, the in-

verse is written as “If you did not prepare your own income tax form, then you received

Cengage

verse is written as “If you did not prepare your own income tax form, then you received

Learning

, then not

Learning

, then not

Learning

CREATING VARIATIONS OFACONDITIONAL STATEMENT

Learning

CREATING VARIATIONS OFACONDITIONAL STATEMENT

ou did not receive the proper refund if you prepared your own

Learning

ou did not receive the proper refund if you prepared your own

income tax form,” write the sentence that represents each of the following.

Learning

income tax form,” write the sentence that represents each of the following.

1.4 More on Conditionals 45

pq~p ~qp→ q q → p ~p → ~q ~q → ~p

TT F F

TF F T

FT T F

FF T T

Required columns in the truth table.FIGURE 1.56

An “if . . . then . . .” statement is false only when the premise is true and the

conclusion is false. Consequently, p → q is false only when p is T and q is F; enter

an F in row 2 and Ts elsewhere in the column under p → q.

Likewise, the converse q → p is false only when q is T and p is F; enter an F

in row 3 and Ts elsewhere.

In a similar manner, the inverse p → q is false only when p is T and q

is F; enter an F in row 3 and Ts elsewhere.

Finally, the contrapositive q → p is false only when q is T and p is F;

enter an F in row 2 and Ts elsewhere.

The completed truth table is shown in Figure 1.57. Examining the entries in

Figure 1.57, we can see that the columns under p → q and q → p are identical;

each has an F in row 2 and Ts elsewhere. Consequently, a conditional and its con-

trapositive are equivalent:

p → q q → p.

Likewise, we notice that q → p and p → q have identical truth values;

each has an F in row 3 and Ts elsewhere. Thus, the converse and the inverse of a

conditional are equivalent:

q → p p → q.

pq~p ~qp→ q q → p ~p → ~q ~q → ~p

TT F F T T T T

TF F T F T T F

FT T F T F F T

FF T T T T T T

Truth table for a conditional and its variations.FIGURE 1.57

We have seen that different “if . . . then . . .” statements can convey the same

meaning—that is, that certain variations of a conditional are equivalent (see Fig-

ure 1.58). For example, the compound statements “If you are compassionate, then

you contribute to charities” and “If you do not contribute to charities, then you are

not compassionate” convey the same meaning. (The second conditional is the con-

trapositive of the ﬁrst.) Regardless of its speciﬁc contents (p, q, p, or q), every

“if . . . then . . .” statement has an equivalent variation formed by negating and in-

terchanging the premise and the conclusion of the given conditional statement.

Equivalent Statements Symbolic Representations

a conditional and its contrapositive ( p → q) ≡ (~q → ~p)

the converse and the inverse (of (q → p) ≡ (~p → ~q)

the conditional p → q)

Equivalent “if . . . then . . .” statements.FIGURE 1.58

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 45

Property

FF T T T T T T

Property

FF T T T T T T

Property

FIGURE 1.57

Property

FIGURE 1.57

TT F F T T T T

TF F T F T T F

FT T F T F F T

TF F T F T T F

Cengage

Figure 1.57, we can see that the columns under

Cengage

Figure 1.57, we can see that the columns under

each has an F in row 2 and Ts elsewhere. Consequently, a conditional and its con-

Cengage

each has an F in row 2 and Ts elsewhere. Consequently, a conditional and its con-

trapositive are equivalent:

Cengage

trapositive are equivalent:

Cengage

→

Cengage

→

Cengage



Cengage



Cengage

Likewise, we notice that

Cengage

Likewise, we notice that

Cengage

→

Cengage

→

each has an F in row 3 and Ts elsewhere. Thus, the converse and the inverse of a

Cengage

each has an F in row 3 and Ts elsewhere. Thus, the converse and the inverse of a

conditional are equivalent:

Cengage

conditional are equivalent:

Cengage

→

Cengage

→

Cengage

~p~

Cengage

~p~

Cengage

TT F F T T T T

Cengage

TT F F T T T T

TF F T F T T F

Cengage

TF F T F T T F

Cengage

TT F F T T T T

Cengage

TT F F T T T T

Cengage

Learning

is false only when

Learning

is false only when

Learning

→

Learning

→

Learning

is false only when

Learning

is false only when

Learning

is T and

Learning

is T and

Learning

is false only when

Learning

is false only when



Learning



Learning

is false only when

Learning

is false only when

enter an F in row 2 and Ts elsewhere.

Learning

enter an F in row 2 and Ts elsewhere.

The completed truth table is shown in Figure 1.57. Examining the entries in

Learning

The completed truth table is shown in Figure 1.57. Examining the entries in

Figure 1.57, we can see that the columns under

Learning

Figure 1.57, we can see that the columns under

each has an F in row 2 and Ts elsewhere. Consequently, a conditional and its con-

Learning

each has an F in row 2 and Ts elsewhere. Consequently, a conditional and its con-

46 CHAPTER 1 Logic

EXAMPLE 4 CREATING A CONTRAPOSITIVE Given the statement “Being a doctor is

necessary for being a surgeon,” express the contrapositive in terms of the

following:

a. a sufﬁcient condition

b. a necessary condition

SOLUTION a. Recalling that a necessary condition is the conclusion of a conditional, we can rephrase

the statement “Being a doctor is necessary for being a surgeon” as follows:

“ a person is a surgeon, the person is a doctor.”

The premise. A necessary condition is

the conclusion.

Therefore, by negating and interchanging the premise and conclusion, the contraposi-

tive is

“ a person is a doctor, the person is a surgeon.”

The negation of The negation of

the conclusion. the premise.

Recalling that a sufﬁcient condition is the premise of a conditional, we can phrase the

contrapositive of the original statement as “Not being a doctor is sufﬁcient for not being

a surgeon.”

b. From part (a), the contrapositive of the original statement is the conditional statement

“ a person is a doctor, the person is a surgeon.”

The premise of The conclusion of

the contrapositive. the contrapositive.

Because a necessary condition is the conclusion of a conditional, the contrapositive

of the (original) statement “Being a doctor is necessary for being a surgeon” can be

expressed as “Not being a surgeon is necessary for not being a doctor.”

The “Only If” Connective

Consider the statement “A prisoner is paroled only if the prisoner obeys the rules.”

What is the premise, and what is the conclusion? Rather than using p and q (which

might bias our investigation), we deﬁne

r: A prisoner is paroled.

s: A prisoner obeys the rules.

The given statement is represented by “r only if s.” Now, “r only if s” means that

r can happen only if s happens. In other words, if s does not happen, then r does not

happen, or s → r. We have seen that s → r is equivalent to r → s. Conse-

quently, “r only if s” is equivalent to the conditional r → s. The premise of the

statement “Aprisoner is paroled only if the prisoner obeys the rules” is “Aprisoner

is paroled,” and the conclusion is “The prisoner obeys the rules.”

The conditional p → q can be phrased “p only if q.” Even though the word if

precedes q, q is not the premise. Whatever follows the connective “only if” is the

conclusion of the conditional.

↑↑

notthennotIf

↑↑

notthennotIf

↑↑

thenIf

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 46

Property

of the (original) statement “Being a doctor is necessary for being a surgeon” can be

Property

of the (original) statement “Being a doctor is necessary for being a surgeon” can be

expressed as “

Property

expressed as “

The “Only If” Connective

Property

The “Only If” Connective

the contrapositive.

Because a necessary condition is the conclusion of a conditional, the contrapositive

of the (original) statement “Being a doctor is necessary for being a surgeon” can be

expressed as “

Not being a surgeon is necessary for not being a doctor.

Cengage

is the

Cengage

is the

premise

Cengage

premise

contrapositive of the original statement as “

Cengage

contrapositive of the original statement as “

Not being a doctor is sufﬁcient for not being

Cengage

Not being a doctor is sufﬁcient for not being

From part (a), the contrapositive of the original statement is the conditional statement

Cengage

From part (a), the contrapositive of the original statement is the conditional statement

“ a person is a doctor, the person is a surgeon.”

Cengage

“ a person is a doctor, the person is a surgeon.”

The premise of

Cengage

The premise of

the contrapositive.

Cengage

the contrapositive.

Because a necessary condition is the conclusion of a conditional, the contrapositive

Cengage

Because a necessary condition is the conclusion of a conditional, the contrapositive

Cengage

↑↑

Cengage

↑↑

Cengage

“ a person is a doctor, the person is a surgeon.”

not

“ a person is a doctor, the person is a surgeon.”

Cengage

“ a person is a doctor, the person is a surgeon.”

not

“ a person is a doctor, the person is a surgeon.”

Cengage

Learning

Therefore, by negating and interchanging the premise and conclusion, the contraposi-

Learning

Therefore, by negating and interchanging the premise and conclusion, the contraposi-

“ a person is a doctor, the person is a surgeon.”

Learning

“ a person is a doctor, the person is a surgeon.”

The negation of

Learning

The negation of

the premise.

Learning

the premise.

premise

Learning

premise

Learning

↑↑

Learning

↑↑

Learning

↑↑

“ a person is a doctor, the person is a surgeon.”

not

“ a person is a doctor, the person is a surgeon.”

Learning

“ a person is a doctor, the person is a surgeon.”

not

“ a person is a doctor, the person is a surgeon.”

Learning

EXAMPLE 5 ANALYZING AN “ONLY IF” STATEMENT For the compound statement

“You receive a federal grant only if your artwork is not obscene,” do the

following:

a. Determine the premise and the conclusion.

b. Rewrite the compound statement in the standard “if . . . then . . .” form.

c. Interpret the conditions that make the statement false.

SOLUTION a. Because the compound statement contains an “only if” connective, the statement that

follows “only if” is the conclusion of the conditional. The premise is “You receive a

federal grant.” The conclusion is “Your artwork is not obscene.”

b. The given compound statement can be rewritten as “If you receive a grant, then your

artwork is not obscene.”

c. First we deﬁne the symbols.

p: You receive a federal grant.

q: Your artwork is obscene.

Then the statement has the symbolic representation p → q. The truth table for

p → q is given in Figure 1.59.

The expression p → q is false under the conditions listed in row 1 (when p and

q are both true). Therefore, the statement “You receive a federal grant only if your

artwork is not obscene” is false when an artist does receive a federal grant and the

artist’s artwork is obscene.

The Biconditional p ↔ q

What do the words bicycle, binomial, and bilingual have in common? Each word

begins with the preﬁx bi, meaning “two.” Just as the word bilingual means “two

languages,” the word biconditional means “two conditionals.”

In everyday speech, conditionals often get “hooked together” in a circular

fashion. For instance, someone might say, “If I am rich, then I am happy, and if I

am happy, then I am rich.” Notice that this compound statement is actually the con-

junction (and) of a conditional (if rich, then happy) and its converse (if happy, then

rich). Such a statement is referred to as a biconditional. A biconditional is a state-

ment of the form (p → q) ∧ (q → p) and is symbolized as p ↔ q. The symbol p ↔ q

is read “p if and only if q” and is frequently abbreviated “p iff q.” A biconditional

is equivalent to the conjunction of two conversely related conditionals:

p ↔ q 

[(p → q) ∧ (q → p)].

In addition to the phrase “if and only if,” a biconditional can also be ex-

pressed by using “necessary” and “sufﬁcient” terminology. The statement “p is

sufﬁcient for q” can be rephrased as “if p then q” (and symbolized as p → q),

whereas the statement “p is necessary for q” can be rephrased as “if q then p” (and

symbolized as q → p). Therefore, the biconditional “p if and only if q” can also be

phrased as “p is necessary and sufﬁcient for q.”

EXAMPLE 6 ANALYZING A BICONDITIONAL STATEMENT Express the biconditional

“A citizen is eligible to vote if and only if the citizen is at least eighteen years old”

as the conjunction of two conditionals.

SOLUTION The given biconditional is equivalent to “If a citizen is eligible to vote, then the

citizen is at least eighteen years old, and if a citizen is at least eighteen years old,

then the citizen is eligible to vote.”

1.4 More on Conditionals 47

pq~qp→ ~q

TT F F

TF T T

FT F T

FF T T

Truth table for the conditional

p → q.

FIGURE 1.59

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 47

Property

fashion. For instance, someone might say, “If I am rich, then I am happy, and if I

Property

fashion. For instance, someone might say, “If I am rich, then I am happy, and if I

am happy, then I am rich.” Notice that this compound statement is actually the con-

Property

am happy, then I am rich.” Notice that this compound statement is actually the con-

junction (

Property

junction (

rich). Such a statement is referred to as a biconditional. A

Property

rich). Such a statement is referred to as a biconditional. A

ment of the form (

Property

ment of the form (

begins with the preﬁx

languages,” the word

In everyday speech, conditionals often get “hooked together” in a circular

fashion. For instance, someone might say, “If I am rich, then I am happy, and if I

Cengage

artwork is not obscene” is false when an artist

Cengage

artwork is not obscene” is false when an artist

The Biconditional

Cengage

The Biconditional

Cengage

What do the words

Cengage

What do the words

bicycle, binomial,

Cengage

bicycle, binomial,

begins with the preﬁx

Cengage

begins with the preﬁx

languages,” the word

Cengage

languages,” the word

In everyday speech, conditionals often get “hooked together” in a circular

Cengage

In everyday speech, conditionals often get “hooked together” in a circular

Learning

Then the statement has the symbolic representation

Learning

Then the statement has the symbolic representation

Learning

is false under the conditions listed in row 1 (when

Learning

is false under the conditions listed in row 1 (when

are both true). Therefore, the statement “You receive a federal grant only if your

Learning

are both true). Therefore, the statement “You receive a federal grant only if your

artwork is not obscene” is false when an artist

Learning

artwork is not obscene” is false when an artist

3. p: I watch television.

q: I do my homework.

4. p: He is an artist.

q: He is a conformist.

In Exercises 5–10, form (a) the inverse, (b) the converse, and (c)

the contrapositive of the given conditional.

5. If you pass this mathematics course, then you fulﬁll a

graduation requirement.

6. If you have the necessary tools, assembly time is less

than thirty minutes.

7. The television set does not work if the electricity is

turned off.

8. You do not win if you do not buy a lottery ticket.

In Exercises 1–2, using the given statements, write the sentence

represented by each of the following.

a. p → q b. q → p

c. p → q d. q → p

e. Which of parts (a)–(d) are equivalent? Why?

1. p: She is a police ofﬁcer.

q: She carries a gun.

2. p: I am a multimillion-dollar lottery winner.

q: I am a world traveler.

In Exercises 3–4, using the given statements, write the sentence

represented by each of the following.

a. p → q b. q → p

c. p → q d. q → p

e. Which of parts (a)–(d) are equivalent? Why?

Under what circumstances is the biconditional p ↔ q true, and when is it

false? To ﬁnd the answer, we must construct a truth table. Utilizing the equivalence

p ↔ q  [(p → q) ∧ (q → p)], we get the completed table shown in Figure 1.60.

(Recall that a conditional is false only when its premise is true and its conclusion

is false and that a conjunction is true only when both components are true.) We can

see that a biconditional is true only when the two components p and q have the

same truth value—that is, when p and q are both true or when p and q are both

false. On the other hand, a biconditional is false when the two components p and q

have opposite truth value—that is, when p is true and q is false or vice versa.

48 CHAPTER 1 Logic

pqp→ qq→ p (p → q) ∧ (q → p)

TT T T T

TF F T F

FT T F F

FF T T T

Truth table for a biconditional p ↔ q.FIGURE 1.60

Many theorems in mathematics can be expressed as biconditionals. For

example, when solving a quadratic equation, we have the following: “The equation

 bx  c  0 has exactly one solution if and only if the discriminant

 4ac  0.” Recall that the solutions of a quadratic equation are

This biconditional is equivalent to “If the equation ax

 bx  c  0 has exactly one

solution, then the discriminant b

 4ac  0, and if the discriminant b

 4ac  0,

then the equation ax

 bx  c  0 has exactly one solution”—that is, one condi-

tion implies the other.

1.4 Exercises

x 

b ; 2b

 4ac

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 48

Property

In Exercises 1–2, using the given statements, write the sentence

Property

In Exercises 1–2, using the given statements, write the sentence

represented by each of the following.

Property

represented by each of the following.

tion implies the other.

Property

tion implies the other.

Property

xercises

Property

xercises

solution, then the discriminant

then the equation

tion implies the other.

Cengage

Many theorems in mathematics can be expressed as biconditionals. For

Cengage

Many theorems in mathematics can be expressed as biconditionals. For

example, when solving a quadratic equation, we have the following: “The equation

Cengage

example, when solving a quadratic equation, we have the following: “The equation

0 has exactly one solution if and only if the discriminant

Cengage

0 has exactly one solution if and only if the discriminant

0.” Recall that the solutions of a quadratic equation are

Cengage

0.” Recall that the solutions of a quadratic equation are

This biconditional is equivalent to “If the equation

Cengage

This biconditional is equivalent to “If the equation

solution, then the discriminant

Cengage

solution, then the discriminant



Cengage



Cengage

Learning

Many theorems in mathematics can be expressed as biconditionals. For

Learning

Many theorems in mathematics can be expressed as biconditionals. For

1.4 Exercises 49

9. You are a vegetarian if you do not eat meat.

10. If chemicals are properly disposed of, the environment

is not damaged.

In Exercises 11–14, express the contrapositive of the given

conditional in terms of (a) a sufﬁcient condition and (b) a

necessary condition.

11. Being an orthodontist is sufﬁcient for being a dentist.

12. Being an author is sufﬁcient for being literate.

13. Knowing Morse code is necessary for operating a

telegraph.

14. Knowing CPR is necessary for being a paramedic.

In Exercises 15–20, (a) determine the premise and conclusion,

(b) rewrite the compound statement in the standard “if . . .

then . . .” form, and (c) interpret the conditions that make the

statement false.

15. I take public transportation only if it is convenient.

16. I eat raw ﬁsh only if I am in a Japanese restaurant.

17. I buy foreign products only if domestic products are

not available.

18. I ride my bicycle only if it is not raining.

19. You may become a U.S. senator only if you are at least

thirty years old and have been a citizen for nine years.

20. You may become the president of the United States

only if you are at least thirty-ﬁve years old and were

born a citizen of the United States.

In Exercises 21–28, express the given biconditional as the

conjunction of two conditionals.

21. You obtain a refund if and only if you have a receipt.

22. We eat at Burger World if and only if Ju Ju’s Kitsch-

Inn is closed.

23. The quadratic equation ax

 bx  c  0 has two dis-

tinct real solutions if and only if b

 4ac  0.

24. The quadratic equation ax

 bx  c  0 has complex

solutions iff b

 4ac  0.

25. A polygon is a triangle iff the polygon has three

sides.

26. A triangle is isosceles iff the triangle has two equal

sides.

27. A triangle having a 90° angle is necessary and sufﬁ-

cient for a

 b

 c

28. A triangle having three equal sides is necessary and

sufﬁcient for a triangle having three equal angles.

In Exercises 29–36, translate the two statements into symbolic

form and use truth tables to determine whether the statements are

equivalent.

29. I cannot have surgery if I do not have health insurance.

If I can have surgery, then I do have health insurance.

30. If I am illiterate, I cannot ﬁll out an application form.

I can ﬁll out an application form if I am not illiterate.

31. If you earn less than $12,000 per year, you are eligible

for assistance.

If you are not eligible for assistance, then you earn at

least $12,000 per year.

32. If you earn less than $12,000 per year, you are eligible

for assistance.

If you earn at least $12,000 per year, you are not

eligible for assistance.

33. I watch television only if the program is educational.

I do not watch television if the program is not

educational.

34. I buy seafood only if the seafood is fresh.

If I do not buy seafood, the seafood is not fresh.

35. Being an automobile that is American-made is sufﬁ-

cient for an automobile having hardware that is not

metric.

Being an automobile that is not American-made is

necessary for an automobile having hardware that is

metric.

36. Being an automobile having metric hardware is sufﬁ-

cient for being an automobile that is not American-

made.

Being an automobile not having metric hardware is

necessary for being an automobile that is American-

made.

In Exercises 37–46, write an equivalent variation of the given

conditional.

37. If it is not raining, I walk to work.

38. If it makes a buzzing noise, it is not working properly.

39. It is snowing only if it is cold.

40. You are a criminal only if you do not obey the law.

41. You are not a vegetarian if you eat meat.

42. You are not an artist if you are not creative.

43. All policemen own guns.

44. All college students are sleep deprived.

45. No convicted felon is eligible to vote.

46. No man asks for directions.

In Exercises 47–52, determine which pairs of statements are

equivalent.

47. i. If Proposition 111 passes, freeways are improved.

ii. If Proposition 111 is defeated, freeways are not

improved.

iii. If the freeways are improved, Proposition 111

passes.

iv. If the freeways are not improved, Proposition 111

does not pass.

48. i. If the Giants win, then I am happy.

ii. If I am happy, then the Giants win.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 49

Property

You obtain a refund if and only if you have a receipt.

Property

You obtain a refund if and only if you have a receipt.

We eat at Burger World if and only if Ju Ju’s Kitsch-

Property

We eat at Burger World if and only if Ju Ju’s Kitsch-

The quadratic equation

Property

The quadratic equation

Property



Property



tinct real solutions if and only if

Property

tinct real solutions if and only if

The quadratic equation

Property

The quadratic equation

solutions iff

Property

solutions iff

Property



Property



Property

A polygon is a triangle iff the polygon has three

Property

A polygon is a triangle iff the polygon has three

In Exercises 21–28, express the given biconditional as the

Cengage

You may become a U.S. senator only if you are at least

Cengage

You may become a U.S. senator only if you are at least

thirty years old and have been a citizen for nine years.

Cengage

thirty years old and have been a citizen for nine years.

You may become the president of the United States

Cengage

You may become the president of the United States

only if you are at least thirty-ﬁve years old and were

Cengage

only if you are at least thirty-ﬁve years old and were

necessary for an automobile having hardware that is

Cengage

necessary for an automobile having hardware that is

metric.

Cengage

metric.

36.

Cengage

36.

Being an automobile having metric hardware is sufﬁ-

Cengage

Being an automobile having metric hardware is sufﬁ-

cient for being an automobile that is not American-

Cengage

cient for being an automobile that is not American-

made.

Cengage

made.

Learning

I do not watch television if the program is not

Learning

I do not watch television if the program is not

I buy seafood only if the seafood is fresh.

Learning

I buy seafood only if the seafood is fresh.

If I do not buy seafood, the seafood is not fresh.

Learning

If I do not buy seafood, the seafood is not fresh.

Being an automobile that is American-made is sufﬁ-

Learning

Being an automobile that is American-made is sufﬁ-

cient for an automobile having hardware that is not

Learning

cient for an automobile having hardware that is not

metric.

Learning

metric.

Being an automobile that is not American-made is

Learning

Being an automobile that is not American-made is

necessary for an automobile having hardware that is

Learning

necessary for an automobile having hardware that is

metric.

Learning

metric.

Exercises 58–62 refer to the following: Assuming that a movie’s

popularity is measured by its gross box ofﬁce receipts, six recently

released movies—M, N, O, P, Q, and R—are ranked from most

popular (ﬁrst) to least popular (sixth). There are no ties. The

ranking is consistent with the following conditions:

• O is more popular than R.

• If N is more popular than O, then neither Q nor R is more

popular than P.

• If O is more popular than N, then neither P nor R is more

popular than Q.

• M is more popular than N, or else M is more popular than O,

but not both.

58. Which one of the following could be the ranking of the

movies, from most popular to least popular?

a. N, M, O, R, P, Q

b. P, O, M, Q, N, R

c. Q, P, R, O, M, N

d. O, Q, M, P, N, R

e. P, Q, N, O, R, M

59. If N is the second most popular movie, then which one

of the following could be true?

a. O is more popular than M.

b. Q is more popular than M.

c. R is more popular than M.

d. Q is more popular than P.

e. O is more popular than N.

60. Which one of the following cannot be the most popu-

lar movie?

a. M

b. N

c. O

d. P

e. Q

61. If R is more popular than M, then which one of the fol-

lowing could be true?

a. M is more popular than O.

b. M is more popular than Q.

c. N is more popular than P.

d. N is more popular than O.

e. N is more popular than R.

62. If O is more popular than P and less popular than Q,

then which one of the following could be true?

a. M is more popular than O.

b. N is more popular than M.

c. N is more popular than O.

d. R is more popular than Q.

e. P is more popular than R.

iii. If the Giants lose, then I am unhappy.

iv. If I am unhappy, then the Giants lose.

49. i. I go to church if it is Sunday.

ii. I go to church only if it is Sunday.

iii. If I do not go to church, it is not Sunday.

iv. If it is not Sunday, I do not go to church.

50. i. I am a rebel if I do not have a cause.

ii. I am a rebel only if I do not have a cause.

iii. I am not a rebel if I have a cause.

iv. If I am not a rebel, I have a cause.

51. i. If line 34 is greater than line 29, I use Schedule X.

ii. If I use Schedule X, then line 34 is greater than

line 29.

iii. If I do not use Schedule X, then line 34 is not

greater than line 29.

iv. If line 34 is not greater than line 29, then I do not

use Schedule X.

52. i. If you answer yes to all of the above, then you

complete Part II.

ii. If you answer no to any of the above, then you do

not complete Part II.

iii. If you completed Part II, then you answered yes to

all of the above.

iv. If you did not complete Part II, then you answered

no to at least one of the above.

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

53. What is a contrapositive?

54. What is a converse?

55. What is an inverse?

56. What is a biconditional?

57. How is an “if . . . then . . .” statement related to an

“only if” statement?

THE NEXT LEVEL

If a person wants to pursue an advanced degree

(something beyond a bachelor’s or four-year

degree), chances are the person must take a stan-

dardized exam to gain admission to a graduate

school or to be admitted into a speciﬁc program.

These exams are intended to measure verbal,

quantitative, and analytical skills that have devel-

oped throughout a person’s life. Many classes and

study guides are available to help people prepare

for the exams. The following questions are typical

of those found in the study guides.

50 CHAPTER 1 Logic

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 50

Property

What is a biconditional?

Property

What is a biconditional?

How is an “if . . . then . . .” statement related to an

Property

How is an “if . . . then . . .” statement related to an

“only if” statement?

Property

“only if” statement?

Property

Cengage

If N is the second most popular movie, then which one

Cengage

If N is the second most popular movie, then which one

of the following could be true?

Cengage

of the following could be true?

O is more popular than M.

Cengage

O is more popular than M.

Cengage

Q is more popular than M.

Cengage

Q is more popular than M.

Cengage

R is more popular than M.

Cengage

R is more popular than M.

Cengage

Q is more popular than P.

Cengage

Q is more popular than P.

Cengage

60.

Cengage

60.

Learning

Which one of the following could be the ranking of the

Learning

Which one of the following could be the ranking of the

movies, from most popular to least popular?

Learning

movies, from most popular to least popular?

Q, P, R, O, M, N

Learning

Q, P, R, O, M, N

O, Q, M, P, N, R

Learning

O, Q, M, P, N, R

P, Q, N, O, R, M

Learning

P, Q, N, O, R, M

If N is the second most popular movie, then which one

Learning

If N is the second most popular movie, then which one

of the following could be true?

Learning

of the following could be true?

1.5 Analyzing Arguments

Objectives

•

Identify a tautology

•

Use a truth table to analyze an argument

Lewis Carroll’s Cheshire Cat told Alice that he was mad (crazy). Alice then asked,

“‘And how do you know that you’re mad?’ ‘To begin with,’ said the cat, ‘a dog’s

not mad. You grant that?’ ‘I suppose so,’ said Alice. ‘Well, then,’ the cat went on,

‘you see a dog growls when it’s angry, and wags its tail when it’s pleased. Now I

growl when I’m pleased, and wag my tail when I’m angry. Therefore I’m mad!’”

Does the Cheshire Cat have a valid deductive argument? Does the conclusion

follow logically from the hypotheses? To answer this question, and others like it,

we will utilize symbolic logic and truth tables to account for all possible combina-

tions of the individual statements as true or false.

Valid Arguments

When someone makes a sequence of statements and draws some conclusion from

them, he or she is presenting an argument. An argument consists of two compo-

nents: the initial statements, or hypotheses, and the ﬁnal statement, or conclusion.

When presented with an argument, a listener or reader may ask, “Does this person

have a logical argument? Does his or her conclusion necessarily follow from the

given statements?”

An argument is valid if the conclusion of the argument is guaranteed under

its given set of hypotheses. (That is, the conclusion is inescapable in all instances.)

For example, we used Venn diagrams in Section 1.1 to show the argument

“All men are mortal.

Socrates is a man.

the hypotheses

Therefore, Socrates is mortal.” the conclusion

is a valid argument. Given the hypotheses, the conclusion is guaranteed. The term

valid does not mean that all the statements are true but merely that the conclusion

was reached via a proper deductive process. As shown in Example 3 of Section 1.1,

the argument

“All doctors are men.

My mother is a doctor.

the hypotheses

Therefore, my mother is a man.”

the conclusion

is also a valid argument. Even though the conclusion is obviously false, the con-

clusion is guaranteed, given the hypotheses.

The hypotheses in a given logical argument may consist of several interrelated

statements, each containing negations, conjunctions, disjunctions, and conditionals.

By joining all the hypotheses in the form of a conjunction, we can form a single con-

ditional that represents the entire argument. That is, if an argument has n hypotheses

, h

,...,h

) and conclusion c, the argument will have the form “if (h

and h

...and

), then c.”

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 51

Property

its given set of hypotheses. (That is, the conclusion is inescapable in all instances.)

Property

its given set of hypotheses. (That is, the conclusion is inescapable in all instances.)

For example, we used Venn diagrams in Section 1.1 to show the argument

Property

For example, we used Venn diagrams in Section 1.1 to show the argument

have a logical argument? Does his or her conclusion necessarily follow from the

given statements?”

An argument is

its given set of hypotheses. (That is, the conclusion is inescapable in all instances.)

Cengage

Valid Arguments

Cengage

Valid Arguments

When someone makes a sequence of statements and draws some conclusion from

Cengage

When someone makes a sequence of statements and draws some conclusion from

them, he or she is presenting an argument. An

Cengage

them, he or she is presenting an argument. An

nents: the initial statements, or hypotheses, and the ﬁnal statement, or conclusion.

Cengage

nents: the initial statements, or hypotheses, and the ﬁnal statement, or conclusion.

When presented with an argument, a listener or reader may ask, “Does this person

Cengage

When presented with an argument, a listener or reader may ask, “Does this person

have a logical argument? Does his or her conclusion necessarily follow from the

Cengage

have a logical argument? Does his or her conclusion necessarily follow from the

given statements?”

Cengage

given statements?”

Learning

“‘And how do you know that you’re mad?’ ‘To begin with,’ said the cat, ‘a dog’s

Learning

“‘And how do you know that you’re mad?’ ‘To begin with,’ said the cat, ‘a dog’s

not mad. You grant that?’ ‘I suppose so,’ said Alice. ‘Well, then,’ the cat went on,

Learning

not mad. You grant that?’ ‘I suppose so,’ said Alice. ‘Well, then,’ the cat went on,

‘you see a dog growls when it’s angry, and wags its tail when it’s pleased. Now

Learning

‘you see a dog growls when it’s angry, and wags its tail when it’s pleased. Now

growl when I’m pleased, and wag my tail when I’m angry. Therefore I’m mad!’”

Learning

growl when I’m pleased, and wag my tail when I’m angry. Therefore I’m mad!’”

ire Cat have a valid deductive argument? Does the conclusion

Learning

ire Cat have a valid deductive argument? Does the conclusion

follow logically from the hypotheses? To answer this question, and others like it,

Learning

follow logically from the hypotheses? To answer this question, and others like it,

we will utilize symbolic logic and truth tables to account for all possible combina-

Learning

we will utilize symbolic logic and truth tables to account for all possible combina-

tions of the individual statements as true or false.

Learning

tions of the individual statements as true or false.

52 CHAPTER 1 Logic

Using a logical argument, Lewis Carroll’s Cheshire Cat tried to

convince Alice that he was crazy. Was his argument valid?

If the conditional representation of an argument is always true (regardless

of the actual truthfulness of the individual statements), the argument is valid. If

there is at least one instance in which the conditional is false, the argument is

invalid.

EXAMPLE 1 USING A TRUTH TABLE TO ANALYZE AN ARGUMENT Determine

whether the following argument is valid:

“If he is illiterate, he cannot ﬁll out the application.

He can ﬁll out the application.

Therefore, he is not illiterate.”

SOLUTION First, number the hypotheses and separate them from the conclusion with a line:

1. If he is illiterate, he cannot ﬁll out the application.

2. He can ﬁll out the application.

Therefore, he is not illiterate.

Now use symbols to represent each different component in the statements:

p: He is illiterate.

q: He can ﬁll out the application.

CONDITIONAL REPRESENTATION OF AN ARGUMENT

An argument having n hypotheses h

, h

...

, h

and conclusion c can be

represented by the conditional [h

∧ h

∧

...

∧ h

] → c.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 52

Property

If the conditional representation of an argument is always true (regardless

Property

If the conditional representation of an argument is always true (regardless

of the actual truthfulness of the individual statements), the argument is valid. If

Property

of the actual truthfulness of the individual statements), the argument is valid. If

there is at least one instance in which the conditional is false, the argument is

Property

there is at least one instance in which the conditional is false, the argument is

invalid.

Property

invalid.

EXAMPLE

Property

EXAMPLE

Property

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

Property

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

Property

If the conditional representation of an argument is always true (regardless

represented by the conditional [

Cengage

Using a logical argument, Lewis Carroll’s Cheshire Cat tried to

Cengage

Using a logical argument, Lewis Carroll’s Cheshire Cat tried to

convince Alice that he was crazy. Was his argument valid

Cengage

convince Alice that he was crazy. Was his argument valid

Cengage

CONDITIONAL REPRESENTATION OF AN ARGUMENT

Cengage

CONDITIONAL REPRESENTATION OF AN ARGUMENT

An argument having

Cengage

An argument having

Cengage

hypotheses

Cengage

hypotheses

represented by the conditional [

Cengage

represented by the conditional [

Cengage

Learning

Using a logical argument, Lewis Carroll’s Cheshire Cat tried to

Learning

Using a logical argument, Lewis Carroll’s Cheshire Cat tried to

Learning

We could have deﬁned q as “He cannot ﬁll out the application” (as stated in prem-

ise 1), but it is customary to deﬁne the symbols with a positive sense. Symboli-

cally, the argument has the form

1. p → q

2. q

the hypotheses

∴ p conclusion

and is represented by the conditional [(p → q) ∧ q] → p. The symbol ∴ is read

“therefore.”

To construct a truth table for this conditional, we need 2

 4 rows. A column

is required for the following: each negation, each hypothesis, the conjunction of

the hypotheses, the conclusion, and the conditional representation of the argument.

The initial setup is shown in Figure 1.61.

Fill in the truth table as follows:

q: A negation has the opposite truth values; enter a T in rows 2 and 4 and an F in

rows 1 and 3.

Hypothesis 1: A conditional is false only when its premise is true and its conclusion

is false; enter an F in row 1 and Ts elsewhere.

⎫

⎬

⎭

⎫

⎬

⎭

1.5 Analyzing Arguments 53

Column Conditional

Representing Representation

Hypothesis Hypothesis All the Conclusion of the

1 2 Hypotheses c Argument

pqqp→ qq 1

∧

2 p (1

∧

2) → c

Required columns in the truth table.FIGURE 1.61

ondon—Devotees of writer Lewis

Carroll believe they have found what

inspired his grinning Cheshire Cat,

made famous in his book “Alice’s Ad-

ventures in Wonderland.”

Members of the Lewis Carroll Society

made the discovery over the weekend in

a church at which the author’s father

was once rector in the Yorkshire village

of Croft in northern England.

It is a rough-hewn carving of a cat’s

head smiling near an altar, probably

dating to the 10th century. Seen from

below and from the perspective of a

small boy, all that can be seen is the

grinning mouth.

Carroll’s Alice watched the Cheshire

Cat disappear “ending with the grin,

Featured In

The news

Reprinted with permission from

Reuters.

which remained for some time after the

rest of the head had gone.”

Alice mused: “I have often seen a cat

without a grin, but not a grin without a

cat. It is the most curious thing I have

seen in all my life.”

CHURCH CARVING MAY BE ORIGINAL

‘CHESHIRE CAT’

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 53

Property

the hypotheses, the conclusion, and the conditional representation of the argument.

Property

the hypotheses, the conclusion, and the conditional representation of the argument.

The initial setup is shown in Figure 1.61.

Property

The initial setup is shown in Figure 1.61.

Fill in the truth table as follows:

Property

Fill in the truth table as follows:

Property

To construct a truth table for this conditional, we need 2

is required for the following: each negation, each hypothesis, the conjunction of

the hypotheses, the conclusion, and the conditional representation of the argument.

The initial setup is shown in Figure 1.61.

Cengage

ise 1), but it is customary to deﬁne the symbols with a positive sense. Symboli-

Cengage

ise 1), but it is customary to deﬁne the symbols with a positive sense. Symboli-

cally, the argument has the form

Cengage

cally, the argument has the form

the hypotheses

Cengage

the hypotheses

conclusion

Cengage

conclusion

and is represented by the conditional [(

Cengage

and is represented by the conditional [(

“therefore.”

Cengage

“therefore.”

To construct a truth table for this conditional, we need 2

Cengage

To construct a truth table for this conditional, we need 2

is required for the following: each negation, each hypothesis, the conjunction of

Cengage

is required for the following: each negation, each hypothesis, the conjunction of

⎫

Cengage

⎫

⎬

Cengage

⎬

⎫

⎬

⎫

Cengage

⎫

⎬

⎫

⎭

Cengage

⎭

⎬

⎭

⎬

Cengage

⎬

⎭

⎬

Cengage

⎬

⎭

Cengage

⎭

⎬

⎭

⎬

Cengage

⎬

⎭

⎬

Learning

Reprinted with permission from

Learning

Reprinted with permission from

Reuters.

Learning

Reuters.

Learning

cannot

Learning

cannot

ﬁll out the application” (as stated in prem-

Learning

ﬁll out the application” (as stated in prem-

ise 1), but it is customary to deﬁne the symbols with a positive sense. Symboli-

Learning

ise 1), but it is customary to deﬁne the symbols with a positive sense. Symboli-

Learning

Hypothesis 2: Recopy the q column.

1 ∧ 2: A conjunction is true only when both components are true; enter a T in row 3

and Fs elsewhere.

Conclusion c: A negation has the opposite truth values; enter an F in rows 1 and 2

and a T in rows 3 and 4.

At this point, all that remains is the ﬁnal column (see Figure 1.62).

54 CHAPTER 1 Logic

12 c

pqqp→ qq1

∧

2 p (1

∧

2) → c

TT F F T F F

TF T T F F F

FT F T T T T

FF T T F F T

Truth values of the expressions.FIGURE 1.62

12 c

pqqp→ qq1

∧

2 p (1

∧

2) → c

TT F F T F F T

TF T T F F F T

FT F T T T T T

FF T T F F T T

Truth table for the argument [(p → q) ∧ q] → p.FIGURE 1.63

The last column in the truth table is the conditional that represents the entire

argument. A conditional is false only when its premise is true and its conclusion is

false. The only instance in which the premise (1 ∧ 2) is true is row 3. Corresponding

to this entry, the conclusion p is also true. Consequently, the conditional (1 ∧ 2) → c

is true in row 3. Because the premise (1 ∧ 2) is false in rows 1, 2, and 4, the condi-

tional (1 ∧ 2) → c is automatically true in those rows as well. The completed truth

table is shown in Figure 1.63.

The completed truth table shows that the conditional [(p → q) ∧ q] → p

is always true. The conditional represents the argument “If he is illiterate, he

cannot ﬁll out the application. He can ﬁll out the application. Therefore, he is not

illiterate.” Thus, the argument is valid.

Tautologies

A tautology is a statement that is always true. For example, the statement

“(a  b)

 a

 2ab  b

”

is a tautology.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 54

Property

TT F F T F F T

Property

TT F F T F F T

Property

TF T T F F F T

Property

TF T T F F F T

Property

FT F T T T T T

Property

FT F T T T T T

Property

TT F F T F F T

Property

TT F F T F F T

Property

TF T T F F F T

Property

TF T T F F F T

Property

Cengage

The last column in the truth table is the conditional that represents the entire

Cengage

The last column in the truth table is the conditional that represents the entire

argument. A conditional is false only when its premise is true and its conclusion is

Cengage

argument. A conditional is false only when its premise is true and its conclusion is

false. The only instance in which the premise (1

Cengage

false. The only instance in which the premise (1

Cengage

is also true. Consequently, the conditional (1

Cengage

is also true. Consequently, the conditional (1

is true in row 3. Because the premise (1

Cengage

is true in row 3. Because the premise (1

is automatically true in those rows as well. The completed truth

Cengage

is automatically true in those rows as well. The completed truth

table is shown in Figure 1.63.

Cengage

table is shown in Figure 1.63.

Learning

FT F T T T T

Learning

FT F T T T T

FF T T F F T

Learning

FF T T F F T

Learning

FF T T F F T

Learning

FF T T F F T

Learning

The last column in the truth table is the conditional that represents the entire

Learning

The last column in the truth table is the conditional that represents the entire

EXAMPLE 2 DETERMINING WHETHER A STATEMENT IS A TAUTOLOGY

Determine whether the statement (p ∧ q) → (p ∨ q) is a tautology.

SOLUTION We need to construct a truth table for the statement. Because there are two letters,

the table must have 2

 4 rows. We need a column for (p ∧ q), one for (p ∨ q),

and one for (p ∧ q) → (p ∨ q). The completed truth table is shown in Figure 1.64.

1.5 Analyzing Arguments 55

pqp∧ qp∨ q (p ∧ q) → ( p ∨ q)

TT T T T

TF F T T

FT F T T

FF F F T

Truth table for the statement (p ∧ q) → (p ∨ q).FIGURE 1.64

Because (p ∧ q) → (p ∨ q) is always true, it is a tautology.

As we have seen, an argument can be represented by a single conditional. If

this conditional is always true, the argument is valid (and vice versa).

EXAMPLE 3 USING A TRUTH TABLE TO ANALYZE AN ARGUMENT Determine

whether the following argument is valid:

“If the defendant is innocent, the defendant does not go to jail. The defendant does

not go to jail. Therefore, the defendant is innocent.”

SOLUTION Separating the hypotheses from the conclusion, we have

1. If the defendant is innocent, the defendant does not go to jail.

2. The defendant does not go to jail.

Therefore, the defendant is innocent.

Now we deﬁne symbols to represent the various components of the statements:

p: The defendant is innocent.

q: The defendant goes to jail.

Symbolically, the argument has the form

1. p → q

2. q

∴ p

and is represented by the conditional [(p → q) ∧ q] → p.

VALIDITY OF AN ARGUMENT

An argument having n hypotheses h

, h

, . . . , h

and conclusion c is valid if

and only if the conditional [h

∧ h

∧ ... ∧ h

] → c is a tautology.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 55

Property

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

Property

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

whether the following ar

Property

whether the following ar

SOLUTION

Property

SOLUTION

Property

An argument having

and only if the conditional [

Cengage

) is always true, it is a tautology.

Cengage

) is always true, it is a tautology.

As we have seen, an argument can be represented by a single conditional. If

Cengage

As we have seen, an argument can be represented by a single conditional. If

this conditional is always true, the argument is valid (and vice versa).

Cengage

this conditional is always true, the argument is valid (and vice versa).

Cengage

VALIDITY OF AN ARGUMENT

Cengage

VALIDITY OF AN ARGUMENT

An argument having

Cengage

An argument having

and only if the conditional [

Cengage

and only if the conditional [

Cengage

Learning

FF F F T

Learning

FF F F T

Learning

∧

Learning

∧

Learning

)

Learning

)

→

Learning

→

(

Learning

(

Learning

∨

Learning

∨

Learning

) is always true, it is a tautology.

Learning

) is always true, it is a tautology.

Now we construct a truth table with four rows, along with the necessary

columns. The completed table is shown in Figure 1.65.

56 CHAPTER 1 Logic

Truth table for the argument [(p → q) ∧ q] → p.FIGURE 1.65

21 c

pqqp→ q 1 ∧ 2 p (1 ∧ 2) → c

TT F F F T T

TF T T T T T

FT F T F F T

FF T T T F F

The column representing the argument has an F in row 4; therefore, the con-

ditional representation of the argument is not a tautology. In particular, the conclu-

sion does not logically follow the hypotheses when both p and q are false (row 4).

The argument is not valid. Let us interpret the circumstances expressed in row 4,

the row in which the argument breaks down. Both p and q are false—that is, the de-

fendant is guilty and the defendant does not go to jail. Unfortunately, this situation

can occur in the real world; guilty people do not always go to jail! As long as it is

possible for a guilty person to avoid jail, the argument is invalid.

The following argument was presented as Example 6 in Section 1.1. In that

section, we constructed a Venn diagram to show that the argument was in fact

valid. We now show an alternative method; that is, we construct a truth table to de-

termine whether the argument is valid.

EXAMPLE 4 USING A TRUTH TABLE TO ANALYZE AN ARGUMENT Determine

whether the following argument is valid: “No snake is warm-blooded. All

mammals are warm-blooded. Therefore, snakes are not mammals.”

SOLUTION Separating the hypotheses from the conclusion, we have

1. No snake is warm-blooded.

2. All mammals are warm-blooded.

Therefore, snakes are not mammals.

These statements can be rephrased as follows:

1. If it is a snake, then it is not warm-blooded.

2. If it is a mammal, then it is warm-blooded.

Therefore, if it is a snake, then it is not a mammal.

Now we deﬁne symbols to represent the various components of the statements:

p: It is a snake.

q: It is warm-blooded.

r: It is a mammal.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 56

Property

termine whether the argument is valid.

Property

termine whether the argument is valid.

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

Property

USING A TRUTH TABLE TO ANALYZE AN ARGUMENT

whether the following argument is valid: “No snake is warm-blooded. All

Property

whether the following argument is valid: “No snake is warm-blooded. All

mammals are warm-blooded. Therefore, snakes are not mammals.”

Property

mammals are warm-blooded. Therefore, snakes are not mammals.”

SOLUTION

Property

SOLUTION

Separating the hypotheses from the conclusion, we have

Property

Separating the hypotheses from the conclusion, we have

Property

section, we constructed a Venn diagram to show that the argument was in fact

valid. We now show an alternative method; that is, we construct a truth table to de-

termine whether the argument is valid.

Cengage

sion does not logically follow the hypotheses when both

Cengage

sion does not logically follow the hypotheses when both

The argument is not valid. Let us interpret the circumstances expressed in row 4,

Cengage

The argument is not valid. Let us interpret the circumstances expressed in row 4,

the row in which the argument breaks down. Both

Cengage

the row in which the argument breaks down. Both

fendant is guilty and the defendant does

Cengage

fendant is guilty and the defendant does

not

Cengage

not

go to jail. Unfortunately, this situation

Cengage

go to jail. Unfortunately, this situation

can occur in the real world; guilty people do not

Cengage

can occur in the real world; guilty people do not

possible for a guilty person to avoid jail, the argument is invalid.

Cengage

possible for a guilty person to avoid jail, the argument is invalid.

The following argument was presented as Example 6 in Section 1.1. In that

Cengage

The following argument was presented as Example 6 in Section 1.1. In that

section, we constructed a Venn diagram to show that the argument was in fact

Cengage

section, we constructed a Venn diagram to show that the argument was in fact

valid. We now show an alternative method; that is, we construct a truth table to de-

Cengage

valid. We now show an alternative method; that is, we construct a truth table to de-

Learning

The column representing the argument has an F in row 4; therefore, the con-

Learning

The column representing the argument has an F in row 4; therefore, the con-

not

Learning

not

a tautology. In particular, the conclu-

Learning

a tautology. In particular, the conclu-

sion does not logically follow the hypotheses when both

Learning

sion does not logically follow the hypotheses when both

The argument is not valid. Let us interpret the circumstances expressed in row 4,

Learning

The argument is not valid. Let us interpret the circumstances expressed in row 4,

Symbolically, the argument has the form

1. p → q

2. r → q

∴ p → r

and is represented by the conditional [(p → q) ∧ (r → q)] → (p → r).

Now we construct a truth table with eight rows (2

 8), along with the nec-

essary columns. The completed table is shown in Figure 1.66.

1.5 Analyzing Arguments 57

12 c

pqrq rp→ qr→ q 1 ∧ 2 p → r (1 ∧ 2) → c

TTT F F F T F F T

TTF F T F T F T T

TFT T F T F F F T

TFF T T T T T T T

FTT F F T T T T T

FTF F T T T T T T

FFT T F T F F T T

FFF T T T T T T T

Truth table for the argument [(p → q) ∧ (r → q)] → (p → r).FIGURE 1.66

The preceding examples contained relatively simple arguments, each con-

sisting of only two hypotheses and two simple statements (letters). In such cases,

many people try to employ “common sense” to conﬁrm the validity of the argu-

ment. For instance, the argument “If it is raining, the streets are wet. It is raining.

Therefore, the streets are wet” is obviously valid. However, it might not be so sim-

ple to determine the validity of an argument that contains several hypotheses and

many simple statements. Indeed, in such cases, the argument’s truth table might

become quite lengthy, as in the next example.

EXAMPLE 5 USING A TRUTH TABLE TO ANALYZE AN ARGUMENT The following

whimsical argument was written by Lewis Carroll and appeared in his 1896 book

Symbolic Logic:

“No ducks waltz. No ofﬁcers ever decline to waltz. All my poultry are ducks.

Therefore, my poultry are not ofﬁcers.”

Construct a truth table to determine whether the argument is valid.

The last column of the truth table represents the argument and contains all T’s.

Consequently, the conditional [(p → q) ∧ (r → q)] → (p → r) is a tautology;

the argument is valid.

95057_01_ch01_p001-066.qxd 9/27/10 9:35 AM Page 57

Property

The last column of the truth table represents the argument and contains all T’s.

Property

The last column of the truth table represents the argument and contains all T’s.

Consequently, the conditional [(

Property

Consequently, the conditional [(

the argument is valid.

Property

the argument is valid.

The last column of the truth table represents the argument and contains all T’s.

Consequently, the conditional [(

Cengage

FTT F F T T T T T

Cengage

FTT F F T T T T T

Cengage

FTF F T T T T T T

Cengage

FTF F T T T T T T

Cengage

FFT T F T F F T T

Cengage

FFT T F T F F T T

FFF T T T T T T T

Cengage

FFF T T T T T T T

Cengage

FTT F F T T T T T

Cengage

FTT F F T T T T T

Cengage

FTF F T T T T T T

Cengage

FTF F T T T T T T

Cengage

FFT T F T F F T T

Cengage

FFT T F T F F T T

Cengage

FFT T F T F F T T

Cengage

FFT T F T F F T T

FFF T T T T T T T

Cengage

FFF T T T T T T T

Cengage

FFF T T T T T T T

Cengage

FFF T T T T T T T

Cengage

Truth table for the argument [(

Cengage

Truth table for the argument [(

Cengage

Learning

∧

Learning

∧

Learning

→

Learning

→

Learning

TTT F F F T F F T

Learning

TTT F F F T F F T

Learning

TTF F T F T F T T

Learning

TTF F T F T F T T

Learning

TFT T F T F F F T

Learning

TFT T F T F F F T

Learning

TFF T T T T T T T

Learning

TFF T T T T T T T

FTT F F T T T T T

Learning

FTT F F T T T T T

Learning

TTT F F F T F F T

Learning

TTT F F F T F F T

Learning

TTF F T F T F T T

Learning

TTF F T F T F T T

Learning

TFT T F T F F F T

Learning

TFT T F T F F F T

Learning

TFF T T T T T T T

Learning

TFF T T T T T T T

FTT F F T T T T T

Learning

FTT F F T T T T T

SOLUTION Separating the hypotheses from the conclusion, we have

1. No ducks waltz.

2. No ofﬁcers ever decline to waltz.

3. All my poultry are ducks.

Therefore, my poultry are not ofﬁcers.

These statements can be rephrased as

1. If it is a duck, then it does not waltz.

2. If it is an ofﬁcer, then it does not decline to waltz.

(Equivalently, “If it is an ofﬁcer, then it will waltz.”)

3. If it is my poultry, then it is a duck.

Therefore, if it is my poultry, then it is not an ofﬁcer.

58 CHAPTER 1 Logic

CHARLES LUTWIDGE DODGSON, 1832–1898

o those who assume that it is

impossible for a person to

excel both in the creative worlds

of art and literature and in the dis-

ciplined worlds of mathematics

and logic, the life of Charles

Lutwidge Dodgson is a wondrous

counterexample. Known the world over

as Lewis Carroll, Dodgson penned the

nonsensical classics Alice’s Adventures in

Wonderland and Through the Looking

Glass. However, many people are sur-

prised to learn that Dodgson (from age

eighteen to his death) was a permanent

resident at the University at Oxford,

teaching mathematics and logic. And as

if that were not enough, Dodgson is now

recognized as one of the leading portrait

photographers of the Victorian era.

The eldest son in a family of eleven

children, Charles amused his younger

siblings with elaborate games, poems,

stories, and humorous drawings. This

attraction to entertaining children with

fantastic stories manifested itself in much

of his later work as Lewis Carroll. Besides

his obvious interest in telling stories, the

young Dodgson was

also intrigued by

mathematics. At the

age of eight, Charles

asked his father to ex-

plain a book on log-

arithms. When told

that he was too

young to understand,

Charles persisted,

“But please, explain!”

The Dodgson family had a strong ec-

clesiastical tradition; Charles’s father,

great-grandfather, and great-great-grand-

father were all clergymen. Following in

his father’s footsteps, Charles attended

Christ Church, the largest and most cele-

brated of all the Oxford colleges. After

graduating in 1854, Charles remained at

Oxford, accepting the position of mathe-

matical lecturer in 1855. However, ap-

pointment to this position was conditional

upon his taking Holy Orders in the Angli-

can church and upon his remaining celi-

bate. Dodgson complied and was

named a deacon in 1861.

The year 1856 was ﬁlled with events

that had lasting effects on Dodgson.

Charles Lutwidge created his pseudonym

by translating his ﬁrst and middle names

into Latin (Carolus Ludovic), reversing their

order (Ludovic Carolus), and translating

them back into English (Lewis Carroll). In

this same year, Dodgson began his

“hobby” of photography. He is consid-

ered by many to have been an artistic pi-

oneer in this new ﬁeld (photography was

invented in 1839). Most of Dodgson’s

work consists of portraits that chronicle the

Victorian era, and over 700 photographs

taken by Dodgson have been preserved.

His favorite subjects were children, espe-

cially young girls.

Dodgson’s afﬁnity for children brought

about a meeting in 1856 that would

eventually establish his place in the his-

tory of literature. Early in the year, Dodg-

son met the four children of the dean of

Christ Church: Harry, Lorina, Edith, and

Alice Liddell. He began seeing the chil-

dren on a regular basis, amusing them

with stories and photographing them. Al-

though he had a wonderful relationship

with all four, Alice received his special

attention.

On July 4, 1862, while rowing and

picnicking with Alice and her sisters,

Dodgson entertained the Liddell girls with

a fantastic story of a little girl named Alice

who fell into a rabbit hole. Captivated by

Historical

Note

95057_01_ch01_p001-066.qxd 9/29/10 3:45 AM Page 58

Property

SOLUTION

Property

SOLUTION

Property

that had lasting effects on Dodgson.

Charles Lutwidge created his pseudonym

by translating his ﬁrst and middle names

Cengage

brated of all the Oxford colleges. After

Cengage

brated of all the Oxford colleges. After

graduating in 1854, Charles remained at

Cengage

graduating in 1854, Charles remained at

Oxford, accepting the position of mathe-

Cengage

Oxford, accepting the position of mathe-

matical lecturer in 1855. However, ap-

Cengage

matical lecturer in 1855. However, ap-

pointment to this position was conditional

Cengage

pointment to this position was conditional

upon his taking Holy Orders in the Angli-

Cengage

upon his taking Holy Orders in the Angli-

can church and upon his remaining celi-

Cengage

can church and upon his remaining celi-

bate. Dodgson complied and was

Cengage

bate. Dodgson complied and was

named a deacon in 1861.

Cengage

named a deacon in 1861.

The year 1856 was ﬁlled with events

Cengage

The year 1856 was ﬁlled with events

that had lasting effects on Dodgson.

Cengage

that had lasting effects on Dodgson.

Charles Lutwidge created his pseudonym

Cengage

Charles Lutwidge created his pseudonym

Learning

Christ Church, the largest and most cele-

Learning

Christ Church, the largest and most cele-

invented in 1839). Most of Dodgson’s

Learning

invented in 1839). Most of Dodgson’s

work consists of portraits that chronicle the

Learning

work consists of portraits that chronicle the

Victorian era, and over 700 photographs

Learning

Victorian era, and over 700 photographs

taken by Dodgson have been preserved.

Learning

taken by Dodgson have been preserved.

His favorite subjects were children, espe-

Learning

His favorite subjects were children, espe-

cially young girls.

Learning

cially young girls.

Dodgson’s afﬁnity for children brought

Learning

Dodgson’s afﬁnity for children brought

about a meeting in 1856 that would

Learning

about a meeting in 1856 that would

eventually establish his place in the his-

Learning

eventually establish his place in the his-

tory of literature. Early in the year, Dodg-

Learning

tory of literature. Early in the year, Dodg-

son met the four children of the dean of

Learning

son met the four children of the dean of

Christ Church: Harry, Lorina, Edith, and

Learning

Christ Church: Harry, Lorina, Edith, and

1.5 Analyzing Arguments 59

Young Alice Liddell inspired Lewis Carroll to

write Alice’s Adventures in Wonderland. This

photo is one of the many Carroll took of Alice.

Carroll’s book The Game of Logic presents the study

of formalized logic in a gamelike fashion. After listing

the “rules of the game” (complete with gameboard

and markers), Carroll captures the reader’s interest

with nonsensical syllogisms.

Brown University Library

the story, Alice Liddell insisted that Dodg-

son write it down for her. He complied,

initially titling it Alice’s Adventure Under-

ground.

Dodgson’s friends subsequently encour-

aged him to publish the manuscript, and in

1865, after editing and inserting new

episodes, Lewis Carroll gave the world

Alice’s Adventures in Wonderland. Al-

though the book appeared to be a whim-

sical excursion into chaotic nonsense,

Dodgson’s masterpiece contained many

exercises in logic and metaphor. The book

was a success, and in 1871, a sequel,

Through the Looking Glass, was printed.

When asked to comment on the meaning

of his writings, Dodgson replied, “I’m very

much afraid I didn’t mean anything but

nonsense! Still, you know, words mean

more than we mean to express when we

use them; so a whole book ought to mean

a great deal more than the writer means.

So, whatever good meanings are in the

book, I’m glad to accept as the meaning

of the book.”

In addition to writing “children’s sto-

ries,” Dodgson wrote numerous mathe-

matics essays and texts, including The

Fifth Book of Euclid Proved Alge-

braically, Formulae of Plane Trigonome-

try, A Guide to the Mathematical Stu-

dent, and Euclid and His Modern Rivals.

In the ﬁeld of formal logic, Dodgson’s

books The Game of Logic (1887) and

Symbolic Logic (1896) are still used as

sources of inspiration in numerous

schools worldwide.

Now we deﬁne symbols to represent the various components of the statements:

p: It is a duck.

q: It will waltz.

r: It is an ofﬁcer.

s: It is my poultry.

Symbolically, the argument has the form

1. p → q

2. r → q

3. s → p

∴ s → r

95057_01_ch01_p001-066.qxd 9/27/10 9:36 AM Page 59

Property

Symbolic Logic

sources of inspiration in numerous

schools worldwide.

Cengage

In addition to writing “children’s sto-

Cengage

In addition to writing “children’s sto-

ries,” Dodgson wrote numerous mathe-

Cengage

ries,” Dodgson wrote numerous mathe-

matics essays and texts, including

Cengage

matics essays and texts, including

Fifth Book of Euclid Proved Alge-

Cengage

Fifth Book of Euclid Proved Alge-

braically, Formulae of Plane Trigonome-

Cengage

braically, Formulae of Plane Trigonome-

try, A Guide to the Mathematical Stu-

Cengage

try, A Guide to the Mathematical Stu-

Euclid and His Modern Rivals.

Cengage

Euclid and His Modern Rivals.

In the ﬁeld of formal logic, Dodgson’s

Cengage

In the ﬁeld of formal logic, Dodgson’s

books

Cengage

books

The Game of Logic

Cengage

The Game of Logic

Symbolic Logic

Cengage

Symbolic Logic

sources of inspiration in numerous

Cengage

sources of inspiration in numerous

Learning

a great deal more than the writer means.

Learning

a great deal more than the writer means.

So, whatever good meanings are in the

Learning

So, whatever good meanings are in the

book, I’m glad to accept as the meaning

Learning

book, I’m glad to accept as the meaning

In addition to writing “children’s sto-

Learning

In addition to writing “children’s sto-

1.5 Exercises

60 CHAPTER 1 Logic

In Exercises 1–10, use the given symbols to rewrite the argument

in symbolic form.

1. p: It is raining.

q: The streets are wet.

}

Use these symbols.

1. If it is raining, then the streets are wet.

2. It is raining.

Therefore, the streets are wet.

2. p: I have a college degree.

q: I am lazy.

}

Use these symbols.

1. If I have a college degree, I am not lazy.

2. I do not have a college degree.

Therefore, I am lazy.

3. p: It is Tuesday.

q: The tour group is in Belgium.

}

Use these symbols.

1. If it is Tuesday, then the tour group is in Belgium.

2. The tour group is not in Belgium.

Therefore, it is not Tuesday.

4. p: You are a gambler.

q: You have ﬁnancial security.

}

Use these symbols.

1. You do not have ﬁnancial security if you are a

gambler.

2. You do not have ﬁnancial security.

Therefore, you are a gambler.

123 c

pqr sq rp→ qr→ qs→ p 1 ∧ 2 ∧ 3 s → r (1 ∧ 2 ∧ 3) → c

TTTT F F F T T F F T

TTTF F F F T T F T T

TT FT F T F T T F T T

TT F F F T F T T F T T

TFTT T F T F T F F T

TFTF T F T F T F T T

TF FT T T T T T T T T

TF FF T T T T T T T T

FTTT F F T T F F F T

FTTF F F T T T T T T

FTFT F T T T F F T T

FTFF F T T T T T T T

FFTT T F T F F F F T

FFTF T F T F T F T T

FFFT T T T T F F T T

FFFF T T T T T T T T

10.

11.

12.

13.

14.

15.

16.

Truth table for the argument [(p → q) ∧ (r → q) ∧ (s → p)] → (s → r).FIGURE 1.67

Now we construct a truth table with sixteen rows (2

 16), along with the neces-

sary columns. The completed table is shown in Figure 1.67.

The last column of the truth table represents the argument and contains all

T’s. Consequently, the conditional [(p → q) ∧ (r → q) ∧ (s → p)] → (s → r) is

a tautology; the argument is valid.

95057_01_ch01_p001-066.qxd 9/27/10 9:36 AM Page 60

Property

xercises

Property

xercises

T’s. Consequently, the conditional [(

Property

T’s. Consequently, the conditional [(

a tautology; the argument is valid.

Property

a tautology; the argument is valid.

Now we construct a truth table with sixteen rows (2

sary columns. The completed table is shown in Figure 1.67.

The last column of the truth table represents the argument and contains all

T’s. Consequently, the conditional [(

Cengage

FFTT T F T F F F F T

Cengage

FFTT T F T F F F F T

Cengage

FFTF T F T F T F T T

Cengage

FFTF T F T F T F T T

Cengage

FFFT T T T T F F T T

Cengage

FFFT T T T T F F T T

FFFF T T T T T T T T

Cengage

FFFF T T T T T T T T

Cengage

FFTT T F T F F F F T

Cengage

FFTT T F T F F F F T

Cengage

FFTF T F T F T F T T

Cengage

FFTF T F T F T F T T

FFFT T T T T F F T T

Cengage

FFFT T T T T F F T T

Cengage

FFFT T T T T F F T T

Cengage

FFFT T T T T F F T T

FFFF T T T T T T T T

Cengage

FFFF T T T T T T T T

Cengage

Truth table for the argument [(

Cengage

Truth table for the argument [(

Cengage

→

Cengage

→



Cengage



Cengage

)

Cengage

)

∧

Cengage

∧

Now we construct a truth table with sixteen rows (2

Cengage

Now we construct a truth table with sixteen rows (2

sary columns. The completed table is shown in Figure 1.67.

Cengage

sary columns. The completed table is shown in Figure 1.67.

Learning

TF FT T T T T T T T T

Learning

TF FT T T T T T T T T

Learning

TF FF T T T T T T T T

Learning

TF FF T T T T T T T T

Learning

FTTT F F T T F F F T

Learning

FTTT F F T T F F F T

Learning

FTTF F F T T T T T T

Learning

FTTF F F T T T T T T

Learning

FTFT F T T T F F T T

Learning

FTFT F T T T F F T T

Learning

FTFF F T T T T T T T

Learning

FTFF F T T T T T T T

FFTT T F T F F F F T

Learning

FFTT T F T F F F F T

Learning

TF FT T T T T T T T T

Learning

TF FT T T T T T T T T

Learning

TF FF T T T T T T T T

Learning

TF FF T T T T T T T T

Learning

FTTT F F T T F F F T

Learning

FTTT F F T T F F F T

Learning

FTTF F F T T T T T T

Learning

FTTF F F T T T T T T

Learning

FTFT F T T T F F T T

Learning

FTFT F T T T F F T T

Learning

FTFF F T T T T T T T

Learning

FTFF F T T T T T T T

17. the argument in Exercise 7

18. the argument in Exercise 8

19. the argument in Exercise 9

20. the argument in Exercise 10

In Exercises 21–42, deﬁne the necessary symbols, rewrite

the argument in symbolic form, and use a truth table to

determine whether the argument is valid. If the argument is

invalid, interpret the speciﬁc circumstances that cause the

argument to be invalid.

21. 1. If the Democrats have a majority, Smith is

appointed and student loans are funded.

2. Smith is appointed or student loans are not funded.

Therefore, the Democrats do not have a majority.

22. 1. If you watch television, you do not read books.

2. If you read books, you are wise.

Therefore, you are not wise if you watch television.

23. 1. If you argue with a police ofﬁcer, you get a ticket.

2. If you do not break the speed limit, you do not get a

ticket.

Therefore, if you break the speed limit, you argue with

a police ofﬁcer.

24. 1. If you do not recycle newspapers, you are not an

environmentalist.

2. If you recycle newspapers, you save trees.

Therefore, you are an environmentalist only if you

save trees.

25. 1. All pesticides are harmful to the environment.

2. No fertilizer is a pesticide.

Therefore, no fertilizer is harmful to the environment.

26. 1. No one who can afford health insurance is unem-

ployed.

2. All politicians can afford health insurance.

Therefore, no politician is unemployed.

27. 1. All poets are loners.

2. All loners are taxi drivers.

Therefore, all poets are taxi drivers.

28. 1. All forest rangers are environmentalists.

2. All forest rangers are storytellers.

Therefore, all environmentalists are storytellers.

29. 1. No professor is a millionaire.

2. No millionaire is illiterate.

Therefore, no professor is illiterate.

30. 1. No artist is a lawyer.

2. No lawyer is a musician.

Therefore, no artist is a musician.

31. 1. All lawyers study logic.

2. You study logic only if you are a scholar.

3. You are not a scholar.

Therefore, you are not a lawyer.

5. p: You exercise regularly.

q: You are healthy.

}

Use these symbols.

1. You exercise regularly only if you are healthy.

2. You do not exercise regularly.

Therefore, you are not healthy.

6. p: The senator supports new taxes.

q: The senator is reelected.

}

1. Thesenatorisnotreelectedifshesupportsnewtaxes.

2. The senator does not support new taxes.

Therefore, the senator is reelected.

7. p: A person knows Morse code.

q: A person operates a telegraph.

}

r: A person is Nikola Tesla.

1. Knowing Morse code is necessary for operating a

telegraph.

2. Nikola Tesla knows Morse code.

Therefore, Nikola Tesla operates a telegraph.

HINT: Hypothesis 2 can be symbolized as r ∧ p.

8. p: A person knows CPR.

q: A person is a paramedic.

r: A person is David Lee Roth.

1. Knowing CPR is necessary for being a paramedic.

2. David Lee Roth is a paramedic.

Therefore, David Lee Roth knows CPR.

HINT: Hypothesis 2 can be symbolized as r ∧ q.

9. p: It is a monkey.

q: It is an ape.

}

Use these symbols.

r: It is King Kong.

1. Being a monkey is sufﬁcient for not being an ape.

2. King Kong is an ape.

Therefore, King Kong is not a monkey.

10. p: It is warm-blooded.

q: It is a reptile.

}

Use these symbols.

r: It is Godzilla.

1. Being warm-blooded is sufﬁcient for not being a

reptile.

2. Godzilla is not warm-blooded.

Therefore, Godzilla is a reptile.

In Exercises 11–20, use a truth table to determine the validity of

the argument speciﬁed. If the argument is invalid, interpret the

speciﬁc circumstances that cause it to be invalid.

11. the argument in Exercise 1

12. the argument in Exercise 2

13. the argument in Exercise 3

14. the argument in Exercise 4

15. the argument in Exercise 5

16. the argument in Exercise 6

Use these

symbols.

}

Use these

symbols.

Use these

symbols.

1.5 Exercises 61

95057_01_ch01_p001-066.qxd 9/27/10 9:36 AM Page 61

Property

Use these symbols.

Property

Use these symbols.

1. Being a monkey is sufﬁcient for not being an ape.

Property

1. Being a monkey is sufﬁcient for not being an ape.

Property

2. King Kong is an ape.

Property

2. King Kong is an ape.

Therefore, King Kong is not a monkey.

Property

Therefore, King Kong is not a monkey.

It is warm-blooded.

Property

It is warm-blooded.

It is a reptile.

Property

It is a reptile.

}

Property

}

It is Godzilla.

Property

It is Godzilla.

1. Being warm-blooded is sufﬁcient for not being a

Property

1. Being warm-blooded is sufﬁcient for not being a

Hypothesis 2 can be symbolized as

Use these symbols.

Cengage

Therefore, if you break the speed limit, you argue with

Cengage

Therefore, if you break the speed limit, you argue with

a police ofﬁcer.

Cengage

a police ofﬁcer.

24.

Cengage

24.

1. If you do not recycle newspapers, you are not an

Cengage

1. If you do not recycle newspapers, you are not an

1. Knowing CPR is necessary for being a paramedic.

Cengage

1. Knowing CPR is necessary for being a paramedic.

Cengage

Hypothesis 2 can be symbolized as

Cengage

Hypothesis 2 can be symbolized as

Cengage

∧

Cengage

∧

Cengage

Learning

2. Smith is appointed or student loans are not funded.

Learning

2. Smith is appointed or student loans are not funded.

Therefore, the Democrats do not have a majority.

Learning

Therefore, the Democrats do not have a majority.

1. If you watch television, you do not read books.

Learning

1. If you watch television, you do not read books.

Learning

2. If you read books, you are wise.

Learning

2. If you read books, you are wise.

Therefore, you are not wise if you watch television.

Learning

Therefore, you are not wise if you watch television.

1. If you argue with a police ofﬁcer, you get a ticket.

Learning

1. If you argue with a police ofﬁcer, you get a ticket.

2. If you do not break the speed limit, you do not get a

Learning

2. If you do not break the speed limit, you do not get a

Learning

ticket.

Learning

ticket.

Therefore, if you break the speed limit, you argue with

Learning

Therefore, if you break the speed limit, you argue with

32. 1. All licensed drivers have insurance.

2. You obey the law if you have insurance.

3. You obey the law.

Therefore, you are a licensed driver.

33. 1. Drinking espresso is sufﬁcient for not sleeping.

2. Not eating dessert is necessary for being on a diet.

3. Not eating dessert is sufﬁcient for drinking espresso.

Therefore, not being on a diet is necessary for sleeping.

34. 1. Not being eligible to vote is sufﬁcient for ignoring

politics.

2. Not being a convicted felon is necessary for being

eligible to vote.

3. Ignoring politics is sufﬁcient for being naive.

Therefore, being naive is necessary being a convicted

felon.

35. If the defendant is innocent, he does not go to jail. The

defendant goes to jail. Therefore, the defendant is guilty.

36. If the defendant is innocent, he does not go to jail. The

defendant is guilty. Therefore, the defendant goes to jail.

37. If you are not in a hurry, you eat at Lulu’s Diner. If you

are in a hurry, you do not eat good food. You eat at

Lulu’s. Therefore, you eat good food.

38. If you give me a hamburger today, I pay you tomorrow.

If you are a sensitive person, you give me a hamburger

today. You are not a sensitive person. Therefore, I do

not pay you tomorrow.

39. If you listen to rock and roll, you do not go to heaven. If

you are a moral person, you go to heaven. Therefore,

you are not a moral person if you listen to rock and roll.

40. If you follow the rules, you have no trouble. If you are

not clever, you have trouble. You are clever. Therefore,

you do not follow the rules.

41. The water not being cold is sufﬁcient for going swim-

ming. Having goggles is necessary for going swim-

ming. I have no goggles. Therefore, the water is cold.

42. I wash my car only if the sky is clear. The sky not being

clear is necessary for it to rain. I do not wash my car.

Therefore, it is raining.

The arguments given in Exercises 43–50 were written by Lewis

Carroll and appeared in his 1896 book Symbolic Logic. For each

argument, deﬁne the necessary symbols, rewrite the argument in

symbolic form, and use a truth table to determine whether the

argument is valid.

43. 1. All medicine is nasty.

2. Senna is a medicine.

Therefore, senna is nasty.

NOTE: Senna is a laxative extracted from the dried

leaves of cassia plants.

44. 1. All pigs are fat.

2. Nothing that is fed on barley-water is fat.

Therefore, pigs are not fed on barley-water.

62 CHAPTER 1 Logic

45. 1. Nothing intelligible ever puzzles me.

2. Logic puzzles me.

Therefore, logic is unintelligible.

46. 1. No misers are unselﬁsh.

2. None but misers save eggshells.

Therefore, no unselﬁsh people save eggshells.

47. 1. No Frenchmen like plum pudding.

2. All Englishmen like plum pudding.

Therefore, Englishmen are not Frenchmen.

48. 1. A prudent man shuns hyenas.

2. No banker is imprudent.

Therefore, no banker fails to shun hyenas.

49. 1. All wasps are unfriendly.

2. No puppies are unfriendly.

Therefore, puppies are not wasps.

50. 1. Improbable stories are not easily believed.

2. None of his stories are probable.

Therefore, none of his stories are easily believed.

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

51. What is a tautology?

52. What is the conditional representation of an argument?

53. Find a “logical” argument in a newspaper article, an

advertisement, or elsewhere in the media. Analyze that

argument and discuss the implications.

•

History Questions

54. What was Charles Dodgson’s pseudonym? How did he

get it? What classic “children’s stories” did he write?

55. What did Charles Dodgson contribute to the study of

formal logic?

56. Charles Dodgson was a pioneer in what artistic ﬁeld?

57. Who was Alice Liddell?

Web project

58. Write a research paper on any historical topic referred

to in this chapter or a related topic. Below is a partial

list of topics.

●

Aristotle

●

George Boole

●

Augustus De Morgan

●

Charles Dodgson/Lewis Carroll

●

Gottfried Wilhelm Leibniz

Some useful links for this web project are listed on the

text web site: www.cengage.com/math/johnson

95057_01_ch01_p001-066.qxd 9/27/10 9:36 AM Page 62

Property

If you follow the rules, you have no trouble. If you are

Property

If you follow the rules, you have no trouble. If you are

not clever, you have trouble. You are clever. Therefore,

Property

not clever, you have trouble. You are clever. Therefore,

The water not being cold is sufﬁcient for going swim-

Property

The water not being cold is sufﬁcient for going swim-

ming. Having goggles is necessary for going swim-

Property

ming. Having goggles is necessary for going swim-

ming. I have no goggles. Therefore, the water is cold.

Property

ming. I have no goggles. Therefore, the water is cold.

I wash my car only if the sky is clear. The sky not being

Property

I wash my car only if the sky is clear. The sky not being

clear is necessary for it to rain. I do not wash my car.

Property

clear is necessary for it to rain. I do not wash my car.

Therefore, it is raining.

Property

Therefore, it is raining.

you are a moral person, you go to heaven. Therefore,

you are not a moral person if you listen to rock and roll.

If you follow the rules, you have no trouble. If you are

not clever, you have trouble. You are clever. Therefore,

Cengage

If you listen to rock and roll, you do not go to heaven. If

Cengage

If you listen to rock and roll, you do not go to heaven. If

you are a moral person, you go to heaven. Therefore,

Cengage

you are a moral person, you go to heaven. Therefore,

Cengage

Therefore, none of his stories are easily believed.

Cengage

Therefore, none of his stories are easily believed.

Answer the following questions using complete

Cengage

Answer the following questions using complete

sentences and your own words.

Cengage

sentences and your own words.

•

Cengage

•

Concept Questions

Cengage

Concept Questions

51.

Cengage

51.

52.

Cengage

52.

Learning

Therefore, no banker fails to shun hyenas.

Learning

Therefore, no banker fails to shun hyenas.

1. All wasps are unfriendly.

Learning

1. All wasps are unfriendly.

Learning

2. No puppies are unfriendly.

Learning

2. No puppies are unfriendly.

Therefore, puppies are not wasps.

Learning

Therefore, puppies are not wasps.

1. Improbable stories are not easily believed.

Learning

1. Improbable stories are not easily believed.

Learning

2. None of his stories are probable.

Learning

2. None of his stories are probable.

Therefore, none of his stories are easily believed.

Learning

Therefore, none of his stories are easily believed.

8. 1. Some animals are dangerous.

2. A gun is not an animal.

Therefore, a gun is not dangerous.

9. 1. Some contractors are electricians.

2. All contractors are carpenters.

Therefore, some electricians are carpenters.

10. Solve the following sudoku puzzle.

11. Explain why each of the following is or is not a

statement.

a. The Golden Gate Bridge spans Chesapeake Bay.

b. The capital of Delaware is Dover.

c. Where are you spending your vacation?

d. Hawaii is the best place to spend a vacation.

12. Determine which pairs of statements are negations of

each other.

a. All of the lawyers are ethical.

b. Some of the lawyers are ethical.

c. None of the lawyers is ethical.

d. Some of the lawyers are not ethical.

REVIEW EXERCISES

TERMS

argument

biconditional

compound statement

conclusion

conditional

conjunction

contrapositive

converse

deductive reasoning

disjunction

equivalent expressions

exclusive or

hypothesis

implication

inclusive or

inductive reasoning

invalid argument

inverse

logic

necessary

negation

premise

quantiﬁer

reasoning

statement

sudoku

sufﬁcient

syllogism

tautology

truth table

truth value

valid argument

Venn diagram

1. Classify each argument as deductive or inductive.

a. 1. Hitchcock’s “Psycho” is a suspenseful movie.

2. Hitchcock’s “The Birds” is a suspenseful movie.

Therefore, all Hitchcock movies are suspenseful.

b. 1. All Hitchcock movies are suspenseful.

2. “Psycho” is a Hitchcock movie.

Therefore, “Psycho” is suspenseful.

2. Explain the general rule or pattern used to assign the

given letter to the given word. Fill in the blank with the

letter that ﬁts the pattern.

3. Fill in the blank with what is most likely to be the next

number. Explain the pattern generated by your answer.

1, 6, 11, 4, _____

In Exercises 4–9, construct a Venn diagram to determine the

validity of the given argument.

4. 1. All truck drivers are union members.

2. Rocky is a truck driver.

Therefore, Rocky is a union member.

5. 1. All truck drivers are union members.

2. Rocky is not a truck driver.

Therefore, Rocky is not a union member.

6. 1. All mechanics are engineers.

2. Casey Jones is an engineer.

Therefore, Casey Jones is a mechanic.

7. 1. All mechanics are engineers.

2. Casey Jones is not an engineer.

Therefore, Casey Jones is not a mechanic.

day morning afternoon dusk night

y r f s _____

Chapter Review

95057_01_ch01_p001-066.qxd 9/28/10 9:39 PM Page 63

Property

Fill in the blank with what is most likely to be the next

Property

Fill in the blank with what is most likely to be the next

number. Explain the pattern generated by your answer.

Property

number. Explain the pattern generated by your answer.

1, 6, 11, 4, _____

Property

1, 6, 11, 4, _____

In Exercises 4–9, construct a Venn diagram to determine the

Property

In Exercises 4–9, construct a Venn diagram to determine the

validity of the given argument.

Property

validity of the given argument.

1. All truck drivers are union members.

Property

1. All truck drivers are union members.

Property

day morning afternoon dusk night

Property

day morning afternoon dusk night

y r f s _____

Property

y r f s _____

Property

day morning afternoon dusk night

Property

day morning afternoon dusk night

y r f s _____

Property

y r f s _____

Property

Explain the general rule or pattern used to assign the

given letter to the given word. Fill in the blank with the

day morning afternoon dusk night

Cengage

1. Some animals are dangerous.

Cengage

1. Some animals are dangerous.

Cengage

2. A gun is not an animal.

Cengage

2. A gun is not an animal.

Therefore, a gun is not dangerous.

Cengage

Therefore, a gun is not dangerous.

Cengage

1. Some contractors are electricians.

Cengage

1. Some contractors are electricians.

Therefore, all Hitchcock movies are suspenseful.

Cengage

Therefore, all Hitchcock movies are suspenseful.

Explain the general rule or pattern used to assign the

Cengage

Explain the general rule or pattern used to assign the

given letter to the given word. Fill in the blank with the

Cengage

given letter to the given word. Fill in the blank with the

Learning

1. Some animals are dangerous.

Learning

1. Some animals are dangerous.

Learning

Venn diagram

Learning

Venn diagram

Learning

In Exercises 18–25, construct a truth table for the compound

statement.

18. p ∨ q 19. p ∧ q

20. p → q 21. (p ∧ q) → q

22. q ∨ (p ∨ r) 23. p → (q ∨ r)

24. (q ∧ p) → (r ∨ p) 25. (p ∨ r) → (q ∧ r)

In Exercises 26–30, construct a truth table to determine whether

the statements in each pair are equivalent.

26. The car is unreliable or expensive.

If the car is reliable, then it is expensive.

27. If I get a raise, I will buy a new car.

If I do not get a raise, I will not buy a new car.

28. She is a Democrat or she did not vote.

She is not a Democrat and she did vote.

29. The raise is not unjustiﬁed and the management

opposes it.

It is not the case that the raise is unjustiﬁed or the

management does not oppose it.

30. Walking on the beach is sufﬁcient for not wearing

shoes. Wearing shoes is necessary for not walking on

the beach.

In Exercises 31–38, write a sentence that represents the negation

of each statement.

31. Jesse had a party and nobody came.

32. You do not go to jail if you pay the ﬁne.

33. I am the winner or you are blind.

34. He is unemployed and he did not apply for ﬁnancial

assistance.

35. The selection procedure has been violated if his

application is ignored.

36. The jackpot is at least $1 million.

37. Drinking espresso is sufﬁcient for not sleeping.

38. Not eating dessert is necessary for being on a diet.

39. Given the statements

p: You are an avid jogger.

q: You are healthy.

write the sentence represented by each of the

following.

a. p → q b. q → p

c. p → q d. q → p

e. p ↔ q

40. Form (a) the inverse, (b) the converse, and (c) the

contrapositive of the conditional “If he is elected, the

country is in big trouble.”

In Exercises 41 and 42, express the contrapositive of the given

conditional in terms of (a) a sufﬁcient condition, and (b) a

necessary condition.

41. Having a map is sufﬁcient for not being lost.

42. Having syrup is necessary for eating pancakes.

13. Write a sentence that represents the negation of each

statement.

a. His car is not new.

b. Some buildings are earthquake proof.

c. All children eat candy.

d. I never cry in a movie theater.

14. Using the symbolic representations

p: The television program is educational.

q: The television program is controversial.

express the following compound statements in symbolic

form.

a. The television program is educational and contro-

versial.

b. If the television program isn’t controversial, it isn’t

educational.

c. The television program is educational and it isn’t

controversial.

d. The television program isn’t educational or

controversial.

e. Not being controversial is necessary for a television

program to be educational.

f. Being controversial is sufﬁcient for a television

program not to be educational.

15. Using the symbolic representations

p: The advertisement is effective.

q: The advertisement is misleading.

r: The advertisement is outdated.

express the following compound statements in symbolic

form.

a. All misleading advertisements are effective.

b. It is a current, honest, effective advertisement.

c. If an advertisement is outdated, it isn’t effective.

d. The advertisement is effective and it isn’t misleading

or outdated.

e. Not being outdated or misleading is necessary for

an advertisement to be effective.

f. Being outdated and misleading is sufﬁcient for an

advertisement not to be effective.

16. Using the symbolic representations

p: It is expensive.

q: It is undesirable.

express the following in words.

a. p → q b. q ↔ p

c. (p ∨ q) d. (p ∧ q) ∨ (p ∧ q)

17. Using the symbolic representations

p: The movie is critically acclaimed.

q: The movie is a box ofﬁce hit.

r: The movie is available on DVD.

express the following in words.

a. (p ∨ q) → r b. (p ∧ q) → r

c. (p ∨ q) ∧ r d. r → (p ∧ q)

64 CHAPTER 1 Logic

95057_01_ch01_p001-066.qxd 9/27/10 9:37 AM Page 64

Property

All misleading advertisements are effective.

Property

All misleading advertisements are effective.

It is a current, honest, effective advertisement.

Property

It is a current, honest, effective advertisement.

If an advertisement is outdated, it isn’t effective.

Property

If an advertisement is outdated, it isn’t effective.

The advertisement is effective and it isn’t misleading

Property

The advertisement is effective and it isn’t misleading

Not being outdated or misleading is necessary for

Property

Not being outdated or misleading is necessary for

an advertisement to be effective.

Property

an advertisement to be effective.

Being outdated and misleading is sufﬁcient for an

Property

Being outdated and misleading is sufﬁcient for an

advertisement not to be effective.

Property

advertisement not to be effective.

Using the symbolic representations

Property

Using the symbolic representations

express the following compound statements in symbolic

All misleading advertisements are effective.

It is a current, honest, effective advertisement.

Cengage

Walking on the beach is sufﬁcient for not wearing

Cengage

Walking on the beach is sufﬁcient for not wearing

shoes. Wearing shoes is necessary for not walking on

Cengage

shoes. Wearing shoes is necessary for not walking on

the beach.

Cengage

the beach.

In Exercises 31–38, write a sentence that represents the negation

Cengage

In Exercises 31–38, write a sentence that represents the negation

of each statement.

Cengage

of each statement.

31.

Cengage

31.

Jesse had a party and nobody came.

Cengage

Jesse had a party and nobody came.

32.

Cengage

32.

You do not go to jail if you pay the ﬁne.

Cengage

You do not go to jail if you pay the ﬁne.

33.

Cengage

33.

express the following compound statements in symbolic

Cengage

express the following compound statements in symbolic

Learning

If I get a raise, I will buy a new car.

Learning

If I get a raise, I will buy a new car.

If I do not get a raise, I will not buy a new car.

Learning

If I do not get a raise, I will not buy a new car.

She is a Democrat or she did not vote.

Learning

She is a Democrat or she did not vote.

She is not a Democrat and she did vote.

Learning

She is not a Democrat and she did vote.

The raise is not unjustiﬁed and the management

Learning

The raise is not unjustiﬁed and the management

It is not the case that the raise is unjustiﬁed or the

Learning

It is not the case that the raise is unjustiﬁed or the

management does not oppose it.

Learning

management does not oppose it.

Walking on the beach is sufﬁcient for not wearing

Learning

Walking on the beach is sufﬁcient for not wearing

shoes. Wearing shoes is necessary for not walking on

Learning

shoes. Wearing shoes is necessary for not walking on

56. 1. Practicing is sufﬁcient for making no mistakes.

2. Making a mistake is necessary for not receiving an

award.

3. You receive an award.

Therefore, you practice.

57. 1. Practicing is sufﬁcient for making no mistakes.

2. Making a mistake is necessary for not receiving an

award.

3. You do not receive an award.

Therefore, you do not practice.

In Exercises 58–66, deﬁne the necessary symbols, rewrite the

argument in symbolic form, and use a truth table to determine

whether the argument is valid.

58. If the defendant is guilty, he goes to jail. The defendant

does not go to jail. Therefore, the defendant is not

guilty.

59. I will go to the concert only if you buy me a ticket.

You bought me a ticket. Therefore, I will go to the

concert.

60. If tuition is raised, students take out loans or drop out.

If students do not take out loans, they drop out.

Students do drop out. Therefore, tuition is raised.

61. If our oil supply is cut off, our economy collapses. If we

go to war, our economy doesn’t collapse. Therefore, if

our oil supply isn’t cut off, we do not go to war.

62. No professor is uneducated. No monkey is educated.

Therefore, no professor is a monkey.

63. No professor is uneducated. No monkey is a professor.

Therefore, no monkey is educated.

64. Vehicles stop if the trafﬁc light is red. There is no

accident if vehicles stop. There is an accident.

Therefore, the trafﬁc light is not red.

65. Not investing money in the stock market is necessary

for invested money to be guaranteed. Invested money

not being guaranteed is sufﬁcient for not retiring at an

early age. Therefore, you retire at an early age only if

your money is not invested in the stock market.

66. Not investing money in the stock market is necessary

for invested money to be guaranteed. Invested money

not being guaranteed is sufﬁcient for not retiring at an

early age. You do not invest in the stock market.

Therefore, you retire at an early age.

Determine the validity of the arguments in Exercises 67 and 68 by

constructing a

a. Venn diagram and a

b. truth table.

c. How do the answers to parts (a) and (b) compare? Why?

67. 1. If you own a hybrid vehicle, then you are an

environmentalist.

2. You are not an environmentalist.

Therefore, you do not own a hybrid vehicle.

In Exercises 43–48, (a) determine the premise and conclusion

and (b) rewrite the compound statement in the standard “if . . .

then . . .” form.

43. The economy improves only if unemployment goes

down.

44. The economy improves if unemployment goes down.

45. No computer is unrepairable.

46. All gemstones are valuable.

47. Being the fourth Thursday in November is sufﬁcient

for the U.S. Post Ofﬁce to be closed.

48. Having diesel fuel is necessary for the vehicle to

operate.

In Exercises 49 and 50, translate the two statements into symbolic

form and use truth tables to determine whether the statements are

equivalent.

49. If you are allergic to dairy products, you cannot eat

cheese.

If you cannot eat cheese, then you are allergic to dairy

products.

50. You are a fool if you listen to me.

You are not a fool only if you do not listen to me.

51. Which pairs of statements are equivalent?

i. If it is not raining, I ride my bicycle to work.

ii. If I ride my bicycle to work, it is not raining.

iii. If I do not ride my bicycle to work, it is raining.

iv. If it is raining, I do not ride my bicycle to work.

In Exercises 52–57, deﬁne the necessary symbols, rewrite the

argument in symbolic form, and use a truth table to determine

whether the argument is valid.

52. 1. If you do not make your loan payment, your car is

repossessed.

2. Your car is repossessed.

Therefore, you did not make your loan payment.

53. 1. If you do not pay attention, you do not learn the

new method.

2. You do learn the new method.

Therefore, you do pay attention.

54. 1. If you rent DVD, you will not go to the movie

theater.

2. If you go to the movie theater, you pay attention to

the movie.

Therefore, you do not pay attention to the movie if you

rent DVDs.

55. 1. If the Republicans have a majority, Farnsworth is

appointed and no new taxes are imposed.

2. New taxes are imposed.

Therefore, the Republicans do not have a majority or

Farnsworth is not appointed.

Chapter Review 65

95057_01_ch01_p001-066.qxd 9/27/10 9:37 AM Page 65

Property

argument in symbolic form, and use a truth table to determine

Property

argument in symbolic form, and use a truth table to determine

1. If you do not make your loan payment, your car is

Property

1. If you do not make your loan payment, your car is

Property

2. Your car is repossessed.

Property

2. Your car is repossessed.

Therefore, you did not make your loan payment.

Property

Therefore, you did not make your loan payment.

1. If you do not pay attention, you do not learn the

Property

1. If you do not pay attention, you do not learn the

new method.

Property

new method.

2. You do learn the new method.

Property

2. You do learn the new method.

In Exercises 52–57, deﬁne the necessary symbols, rewrite the

argument in symbolic form, and use a truth table to determine

Cengage

concert.

Cengage

concert.

60.

Cengage

60.

If tuition is raised, students take out loans or drop out.

Cengage

If tuition is raised, students take out loans or drop out.

If students do not take out loans, they drop out.

Cengage

If students do not take out loans, they drop out.

Students do drop out. Therefore, tuition is raised.

Cengage

Students do drop out. Therefore, tuition is raised.

61.

Cengage

61.

If I ride my bicycle to work, it is not raining.

Cengage

If I ride my bicycle to work, it is not raining.

If I do not ride my bicycle to work, it is raining.

Cengage

If I do not ride my bicycle to work, it is raining.

If it is raining, I do not ride my bicycle to work.

Cengage

If it is raining, I do not ride my bicycle to work.

In Exercises 52–57, deﬁne the necessary symbols, rewrite the

Cengage

In Exercises 52–57, deﬁne the necessary symbols, rewrite the

Learning

In Exercises 58–66, deﬁne the necessary symbols, rewrite the

Learning

In Exercises 58–66, deﬁne the necessary symbols, rewrite the

argument in symbolic form, and use a truth table to determine

Learning

argument in symbolic form, and use a truth table to determine

whether the argument is valid.

Learning

whether the argument is valid.

If the defendant is guilty, he goes to jail. The defendant

Learning

If the defendant is guilty, he goes to jail. The defendant

does not go to jail. Therefore, the defendant is not

Learning

does not go to jail. Therefore, the defendant is not

I will go to the concert only if you buy me a ticket.

Learning

I will go to the concert only if you buy me a ticket.

You bought me a ticket. Therefore, I will go to the

Learning

You bought me a ticket. Therefore, I will go to the

concert.

Learning

concert.

71. a. What is a sufﬁcient condition?

b. What is a necessary condition?

72. What is a tautology?

73. When constructing a truth table, how do you determine

how many rows to create?

•

History Questions

74. What role did the following people play in the

development of formalized logic?

●

Aristotle

●

George Boole

●

Augustus De Morgan

●

Charles Dodgson

●

Gottfried Wilhelm Leibniz

68. 1. If you own a hybrid vehicle, then you are an

environmentalist.

2. You are an environmentalist.

Therefore, you own a hybrid vehicle.

Answer the following questions using complete

sentences and your own words.

•

Concept Questions

69. What is a statement?

70. a. What is a disjunction? Under what conditions is a

disjunction true?

b. What is a conjunction? Under what conditions is a

conjunction true?

c. What is a conditional? Under what conditions is a

conditional true?

d. What is a negation? Under what conditions is a

negation true?

66 CHAPTER 1 Logic

95057_01_ch01_p001-066.qxd 9/27/10 9:37 AM Page 66

Property

Cengage

Learning

Gottfried Wilhelm Leibniz

Learning

Gottfried Wilhelm Leibniz